13.3
Impact Factor
Theranostics 2013; 3(10):774-786. doi:10.7150/thno.5138 This issue Cite
Review
Model Observers in Medical Imaging Research
US Food and Drug Administration.
Received 2012-8-31; Accepted 2013-4-15; Published 2013-10-4
Abstract
Model observers play an important role in the optimization and assessment of imaging devices. In this review paper, we first discuss the basic concepts of model observers, which include the mathematical foundations and psychophysical considerations in designing both optimal observers for optimizing imaging systems and anthropomorphic observers for modeling human observers. Second, we survey a few state-of-the-art computational techniques for estimating model observers and the principles of implementing these techniques. Finally, we review a few applications of model observers in medical imaging research.
Keywords: model observer, medical imaging research
Introduction
Traditionally, medical image quality is defined in terms of measurable physical properties of the medical images, such as resolution, contrast, noise power spectrum, etc. State-of-the-art medical image quality assessment methods take a different philosophical approach by defining the image quality in terms of how well the desired information for a given task of interest can be extracted from the images (1). Specifically, medical image quality is measured by the performance of an observer in conducting a task of clinical interest (1-3). Examples of clinically relevant tasks may include classification tasks, such as a task that requires classifying patients into normal vs. diseased, or estimation tasks, such as a task that requires estimating the volume of a tumor. This is called a statistical, task-based assessment approach (3). The philosophy of the task-based assessment is the corner stone of image science, in which mathematical and statistical theories are used to articulate and formulate the philosophy into symbolic languages - the equations (3). These theories and equations provide the foundations for the large body of research and applications in task-based medical image quality assessment, an essential component of medical imaging practice.
The four key elements of the task-based assessment are: a task of interest, a specification of the population, an appropriate observer, and a figure-of-merit (FOM) (1-3). To perform a rigorous task-based assessment of image quality, these four elements must be carefully considered. For example, a diagnostic task using medical images is often modeled as a binary classification task for classifying patients into diseased vs. normal. In this example, an ensemble of images from both normal and abnormal patients serves as the population. The images in the population should be read by an appropriate observer, either a mathematical model or a real human. Finally, an appropriate FOM is necessary to tell how well the observer performs. In a typical classification study, a receiver operating characteristics (ROC) curve is used to characterize the performance of an observer and the area under the ROC curve (AUC) value is used as the FOM. As a more practical example, the quality of mammographic images is assessed by measuring the average performance of radiologists in a tumor detection task. In this example, the data are images obtained from a representative population of patients with and without breast tumors. The gold standard for tumor presence is usually provided by biopsy. A sufficient number of radiologists will serve as the observers. In a well-controlled laboratory observer study, the clinical tumor detection task is simplified as one that requires the radiologists to classify images into having normal tissues or malignant tumors. A multi-reader multi-case (MRMC) ROC analysis is often used to compute the reader-averaged AUC value and its variance in order to make sure that the study result is generalizable (4-8).
In this paper, our focus is on the third element of task-based image quality assessment: the observers. In particular, we review mathematical model observers in detail. Generally there are two lines of model-observer research. One is in medical imaging, as will be discussed in this paper. The other is in vision science, where the focus is to use model observers as tools to construct principled hypotheses for the purpose of understanding (instead of predicting) the responses of the human visual systems (9-11), such as eye movement (12), crowding(13), illusion(14), etc. Many model-observer concepts in medical imaging originally came from vision-science research. Therefore, although this paper will not cover the related topics in vision science, we encourage interested readers to explore that direction.
In medical imaging, model observers are developed for two general purposes. The first purpose is hardware system optimization. For this purpose, it is desirable to have a model observer that extracts as much statistical information as possible from the images for a given task of interest. For signal detection, the Bayesian ideal observer (IO) or ideal linear observer is often used (3). It has been applied to various modalities, aiming at investigating how system parameters affect signal detection in the presence of noise and other physical factors that degrade image quality (15-17). The second purpose is the evaluation and optimization of software systems, such as image reconstruction or processing methods. For this purpose, it is desirable to study their effects on human-observer performance, because human observers are the end users of software systems. Human-observer studies, however, are resource demanding, especially when our goal is to study the effects of multiple treatments (e.g. multiple parameters for reconstruction algorithms or acquisition protocols) on image quality. In addition, there is a significant amount of variability in human-observer performance. For example, it is observed that different observers may have quite different performance depending on their experience level. Even for the same observer, he/she may fail to give consistent ratings on the same images due to the existence of reader “jitter”. It is thus desirable to design model observers that predict human-observer performance in a consistent manner. Please refer to (18) for an example of the effects of reader variability.
This paper will be organized as follows. In Section I, we will discuss the foundations of model observers in binary classification tasks. Then, in Section II, the difficulties in implementing model observers and state-of-the-art computational techniques will be described. Finally in Section III, we will cover a few applications of model observers in medical imaging research. For the readers' convenience, Table 1 provides a list of abbreviations used in this paper.
Table of Abbreviations.
| Acronyms | Full name |
|---|---|
| FOM | figure-of-merit |
| ROC | receiver operating characteristics |
| AUC | area under ROC curve |
| IO | ideal observer |
| SKE | signal known exactly |
| SKS | signal know statistically |
| BKE | background known exactly |
| BKS | background known statistically |
| probability density function | |
| HO | Hotelling observer |
| SNR | signal-to-noise ratio |
| CIO | channelized ideal observer |
| CHO | channelized Hotelling observer |
| LR | likelihood ratio |
| MCMC | Markov chain Monte Carlo |
| LG | Laguerre Gauss |
| SV | Singular vector |
| PLS | partial least square |
| MRMC | multi-reader multi-case |
Mathematical and Psychophysical Foundations
In the following, we briefly introduce the foundations of various model observers. In particular, we focus on the rationales behind the design of each model observer.
Imaging formation and binary classification tasks
In imaging, the process of data acquisition is represented mathematically as (3)
(1)
where 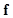 is the object being imaged,
is the object being imaged, 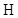 denotes the imaging operator which represents the imaging system,
denotes the imaging operator which represents the imaging system, 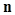 is the noise generated during the measurement, and
is the noise generated during the measurement, and 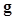 is the image vector. In nuclear-medicine imaging, for example, the object
is the image vector. In nuclear-medicine imaging, for example, the object 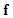 may be the continuous three-dimensional radioactivity distribution in a patient. The imaging system
may be the continuous three-dimensional radioactivity distribution in a patient. The imaging system 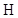 describes the mapping from the continuous object
describes the mapping from the continuous object 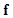 to the discrete image
to the discrete image 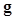 . For an
. For an 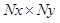 image, the image vector
image, the image vector 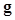 is
is 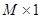 in dimension, where
in dimension, where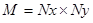 . The random noise
. The random noise 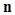 is Poisson in the example of nuclear medicine.
is Poisson in the example of nuclear medicine.
In a binary classification task, there exist two possible hypotheses for a given image: 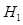 , signal present (e.g. tumor present) or
, signal present (e.g. tumor present) or 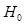 , signal absent (e.g. normal tissue). We mathematically formulate imaging under the two hypotheses as,
, signal absent (e.g. normal tissue). We mathematically formulate imaging under the two hypotheses as,
(2)
where 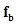 denotes the background object and
denotes the background object and 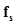 the signal object. These objects could be either known exactly or statistically. A task in which the signal is known exactly is often referred to as a signal-known-exactly (SKE) task. Similarly, there are signal-known-statistically (SKS), background-known-exactly (BKE) and background-known-statistically (BKS) tasks. For mathematical convenience, in model-observer literature the noise-free background and signal images are often defined to be,
the signal object. These objects could be either known exactly or statistically. A task in which the signal is known exactly is often referred to as a signal-known-exactly (SKE) task. Similarly, there are signal-known-statistically (SKS), background-known-exactly (BKE) and background-known-statistically (BKS) tasks. For mathematical convenience, in model-observer literature the noise-free background and signal images are often defined to be,
(3)
respectively.
The ideal observer
In the context of binary classification tasks, the IO is defined as “the observer that utilizes all statistical information available regarding the task to maximize task performance as measured by Bayes risk or some other related measures of performance” (3). If the probability density functions (PDFs) of the raw data 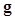 are known under both hypotheses, the IO is the one that uses the likelihood ratio (LR) of
are known under both hypotheses, the IO is the one that uses the likelihood ratio (LR) of 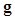 as the decision variable,
as the decision variable,
(4)
where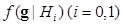 is the PDF of the image vector under the ith hypothesis. For the population from which
is the PDF of the image vector under the ith hypothesis. For the population from which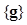 is drawn, the IO defined in (4) provides an upper bound against which all other observers (either model or human) can be compared. Specifically, this IO results in the highest ROC curve among all the other observers who use
is drawn, the IO defined in (4) provides an upper bound against which all other observers (either model or human) can be compared. Specifically, this IO results in the highest ROC curve among all the other observers who use 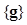 as the data.
as the data.
Due to its optimality, the IO is desirable for use in hardware system optimization. The immediate users of an imaging system are image processing software systems, the purpose of which is to change the representation of the images to help improve the human perception of the images (e.g., tomography reconstruction images enable radiologists to perceive tumors better compared to projection images). Therefore, to maximize the amount of statistical information that will be processed by a software system, it is desirable to optimize an imaging system based on the IO performance.
Hotelling observer (HO) and ideal linear observer
From linear discriminant analysis we derive the Hotelling observer, which is the optimal linear observer when SNR is used as the figure-of-merit (FOM). A linear observer applies a linear template to an image data vector to obtain the value of a scalar test statistic t. In other words, the linear observer uses the test statistic t as the decision variable. That is,
(5)
where is the template of the linear observer, a vector with dimension equal to that of
is the template of the linear observer, a vector with dimension equal to that of 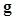 . To quantify the ability of the linear observer in classifying the two classes, the signal-to-noise ratio (SNR) is often used as a FOM,
. To quantify the ability of the linear observer in classifying the two classes, the signal-to-noise ratio (SNR) is often used as a FOM,
(6)
where 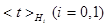 is the mean of the test statistics under each hypothesis and
is the mean of the test statistics under each hypothesis and 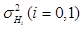 is the variance of the test statistics under each hypothesis. The HO is a linear observer that maximizes the
is the variance of the test statistics under each hypothesis. The HO is a linear observer that maximizes the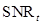 in (6). To do so, the Hotelling template takes the form:
in (6). To do so, the Hotelling template takes the form:
(7)
where 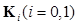 is the covariance matrix of the random image vector
is the covariance matrix of the random image vector 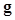 under the ith hypothesis, and
under the ith hypothesis, and 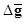 is the difference between the ensemble mean vectors under the two hypotheses.
is the difference between the ensemble mean vectors under the two hypotheses.
The HO is the same as the ideal linear observer when the image vector 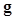 follows multivariate Gaussian distributions with equal covariance matrices under both hypotheses. Note that in this case, the ideal linear observer is the Bayesian ideal observer, and the log of the LR defined in (4) is a linear function of the data vector
follows multivariate Gaussian distributions with equal covariance matrices under both hypotheses. Note that in this case, the ideal linear observer is the Bayesian ideal observer, and the log of the LR defined in (4) is a linear function of the data vector 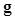 and is expressed as,
and is expressed as,
(8)
where 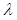 is called the log LR,
is called the log LR, 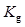 is the ensemble covariance matrix, which is equal between the two classes, and
is the ensemble covariance matrix, which is equal between the two classes, and 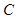 is a constant that is independent of
is a constant that is independent of 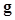 , and thus does not affect the performance of this observer. As a result, the test statistic, or decision variable, used by the ideal linear observer can be expressed as,
, and thus does not affect the performance of this observer. As a result, the test statistic, or decision variable, used by the ideal linear observer can be expressed as,
(9)
Substituting (9) into (6), one can show that the 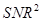 of the ideal linear observer is expressed as,
of the ideal linear observer is expressed as,
(10)
In comparison, the 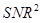 of a HO is expressed as
of a HO is expressed as
(11)
In HO studies, it is a common practice to use independent datasets to train and test the HO. As a result, the first 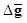 in (10) is calculated using the sample means in the training dataset and the second
in (10) is calculated using the sample means in the training dataset and the second 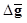 is calculated using the sample means in the testing dataset (19).
is calculated using the sample means in the testing dataset (19).
Note that although the Hotelling observer and the ideal linear observer take similar forms, they are two different observers. The Hotelling observer is optimal with respect to the SNR and its template is calculated using the sample means and variance. The ideal linear observer is an ideal observer whose data follow multi-variate Gaussian distributions. It is optimal in terms of both the SNR and the AUC value. Its template is calculated using the population statistics. For example, in (7), the HO template is calculated using the difference of the sample means, and in (9), the ideal linear observer's template is calculated using the difference of the population means.
In addition to the Hotelling observer and the ideal linear observer mentioned above, another interesting linear observer is the ideal observer for data with Poisson statistics. In particular, in a BKE task, when the data statistics only depends on the Poisson noise, the data distributions under 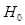 and
and 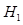 hypotheses are expressed as:
hypotheses are expressed as:
(12)
and,
(13)
where 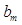 and
and 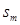 represents the mth pixel on the background or signal image, respectively. The log likelihood ratio is expressed as
represents the mth pixel on the background or signal image, respectively. The log likelihood ratio is expressed as
(14)
where symbol represents Hadamard product and
represents Hadamard product and 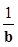 is the element wise inverse assuming
is the element wise inverse assuming 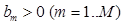 .
.
In this example, we see that the ideal observer of data with Poisson statistics is also a linear observer and it is optimal in terms of the AUC value. However, it is not optimal in terms of the SNR and thus its performance is quite different from the HO. Note that when there are background variations, even if the quantum noise is Poisson, the data statistics is no longer Poisson. Thus the ideal observer is no longer linear.
Channelized observers
The addition of a channel mechanism was originally proposed to predict human-observer performance by incorporating the frequency-domain channels that are thought to exist in the human visual systems (20). It was then found that the appropriate selection of channels can greatly reduce the dimensionality of the HO or IO computation while still approximating the corresponding HO or IO performance. In this section, we discuss the basic principles for applying channels, and the selection of channels will be discussed in the next section.
The application of channels involves multiplying the images with a series of channel template images. Assume a total of L channel images and every channel image is in the format of a 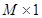 dimensional vector, applying each channel vector to the image vector results in one scalar response, i.e.,
dimensional vector, applying each channel vector to the image vector results in one scalar response, i.e.,
(15)
where 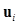 is ith channel and
is ith channel and 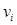 is the ith channel response. Stacking the channel responses together results in a channelized data vector
is the ith channel response. Stacking the channel responses together results in a channelized data vector 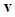 ,
,
(16)
A channelized ideal observer (CIO) or channelized Hotelling observer (CHO) is one that uses the channelized data vector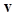 as the data instead of using the image vector
as the data instead of using the image vector 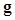 . Thus the decision variable or test statistics of both the CIO or CHO can be computed by replacing
. Thus the decision variable or test statistics of both the CIO or CHO can be computed by replacing 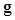 with
with 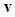 in (4) or (9), resulting in performing the computational task in a space of a much smaller dimension and thus requiring many fewer images for the statistical significance of observer performance estimates.
in (4) or (9), resulting in performing the computational task in a space of a much smaller dimension and thus requiring many fewer images for the statistical significance of observer performance estimates.
Channels
Now the question is what types of channels are available and how to select channels for the given problem. We categorize channels into two groups: anthropomorphic and efficient.
Anthropomorphic channels are used to incorporate the characteristics of the human visual system into a model observer. One of the most widely used characteristics is the spatial-frequency-selective feature, which refers to the mechanisms or “channels” that cause the human visual system to be selectively sensitive to different limited ranges of spatial frequencies (21). The design of spatial-frequency-selective channels usually has three conditions: 1) zero response at zero frequency in the frequency domain; 2) sparse channels (only a handful of channels); and 3) overlapping bandwidths that are octavely spaced, i.e., the width of the Nth channel are twice those of the (N-1)th channel (22). In other words, one averages over more frequencies when sensing higher frequencies (e.g. the Nth channel). Note that satisfying these conditions does not necessarily make channels anthropomorphic; psychophysical studies are a must to validate these channels for the given tasks and image statistics. There are a number of channel models in the literature that have been shown to predict human-observer performance well, such as square channels (Figure 1) (20, 21, 23), difference-of-Gaussians channels (24), difference-of-Mesa filters (25) and Gabor channels (26).
Four square frequency-domain channels and their spatial-domain counterparts shifted to a specific signal centroid location. They are called “square” because they are band-pass filters in the frequency domain and thus their profiles look square along the x or y axis. (Reproduction of Fig. 8 in (27))

Efficient channels are another important concept to consider. Channels are called efficient if the resulting channelized observer approximates the performance of the given unconstrained observer while reducing the data dimension with as few channels as possible (3).
Efficient channels are used to estimate the IO performance (either nonlinear or linear). To find a set of efficient channels for a model observer, one should consider the physics of the imaging system as well as the signal and background data statistics in the task. A practical principle for efficient channel design is to choose a finite number of functions from a large set of basis functions that are used to represent high-dimensional matrices, such as an ensemble of images (28), an imaging system matrix (29), or a Hotelling template (30).
Using all functions of a complete basis, high dimensional matrices can be described exactly. Using only a limited number of the basis functions or an incomplete basis may result in dimension reduction at the expense of information loss. Thus, one might wonder whether the CIO or CHO with efficient channels results in a biased estimate of the unconstrained IO or HO performance. Witten et al. showed that when the background was modeled as identically-independently-distributed Gaussian noise, only one channel was enough to capture all the information for signal detection. Witten et al. also showed that for detecting certain symmetric and asymmetric Gaussian signals in non-Gaussian backgrounds, many more channels (basis functions) were required for representing the background than the signal, and fewer signal-based channels did better than the background-based channels in approximating the unconstrained Bayesian ideal observer (29). This suggests that there is redundant information in the images for the purpose of signal detection and the redundancy is likely related to the complexity of the signal and background statistics. Careful selection of efficient channels may result in an unbiased estimate of the performance of the corresponding unconstrained IO or HO.
Other performance degrading models
Ideal linear observers typically outperform humans (26). The same is true for non-linear IOs. To predict human-observer performance, a typical practice is to degrade the model performance empirically to track human performance or to match human-performance trends by incorporating the characteristics of the human visual systems into the design of model observers. The channel mechanism is probably the most important performance degrading model (5, 20, 21, 23-26). In addition to channels, a few other models are frequently used in the literature, such as internal noise (31), excitatory nonlinearity, inhibitory linearity (26), and human-contrast sensitivity (32), etc.
Next to the channel mechanism discussed in the previous section, internal noise is probably the second most widely used model for degrading model-observer performance to match human performance. It is usually added to the test statistic as a summary of all the degrading factors. That is,
(17)
Comparing (17) to (15), 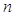 is the internal noise. It is modeled as a random variable with zero-mean. Furthermore, it is generally assumed to be uncorrelated with the image. The choice for the internal noise component has been made empirically on the basis of the absolute performance of one human observer or the average of multiple human observers (24).
is the internal noise. It is modeled as a random variable with zero-mean. Furthermore, it is generally assumed to be uncorrelated with the image. The choice for the internal noise component has been made empirically on the basis of the absolute performance of one human observer or the average of multiple human observers (24).
Performance measures
The AUC, 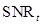 and
and 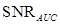 are the three widely used performance FOMs, to be explained below. There are two main approaches used for estimating these performance FOMs. The first is to estimate the test statistics of a finite set of sample images, calculate the AUC using parametric or non-parametric approaches, and convert the AUC estimate to the
are the three widely used performance FOMs, to be explained below. There are two main approaches used for estimating these performance FOMs. The first is to estimate the test statistics of a finite set of sample images, calculate the AUC using parametric or non-parametric approaches, and convert the AUC estimate to the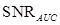 ,
,
(18)
where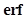 is the Gauss error function. The second one is to compute the
is the Gauss error function. The second one is to compute the 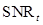 value directly from the sample mean and variance via Eq. (6), and then use (19) to calculate the AUC,
value directly from the sample mean and variance via Eq. (6), and then use (19) to calculate the AUC,
(19)
When the test statistics follow multivariate Gaussian distributions with equal variances, it can be proven using Eqs. (6) and (11) that the 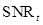 equals
equals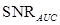 . In addition, they are monotonically related to the AUC. As a result, all three FOMs are valid in performance evaluation. When the normality assumption does not hold, the AUC and
. In addition, they are monotonically related to the AUC. As a result, all three FOMs are valid in performance evaluation. When the normality assumption does not hold, the AUC and 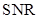 are not necessarily monotonically related. For example, in the previous section, we discussed the linear observer derived for data with Poisson statistics. Since the linear template in (14) is different from the Hotelling template, the linear observer in (14) is not the optimal observer with respect to SNR. However, since it is an ideal observer who uses log-LR as the decision variable, it is optimal with respect to AUC. Which FOM gives an “objective” performance ranking then? This is a challenge that needs to be addressed in a principled way.
are not necessarily monotonically related. For example, in the previous section, we discussed the linear observer derived for data with Poisson statistics. Since the linear template in (14) is different from the Hotelling template, the linear observer in (14) is not the optimal observer with respect to SNR. However, since it is an ideal observer who uses log-LR as the decision variable, it is optimal with respect to AUC. Which FOM gives an “objective” performance ranking then? This is a challenge that needs to be addressed in a principled way.
Advanced tasks
In addition to the binary classification tasks mentioned above, there are other clinically relevant tasks of practical interest. These tasks include general classification tasks with more than two classes(33), estimation tasks (34, 35), localization tasks(36), and the combinations of the aforementioned tasks (37, 38).
Human observers
One important direction in model-observer research is to model human-observer performance. Properties of human observers have been widely studied. It is known that there is a significant amount of intra-observer and inter-observer variability in human-observer performance. In a recent study, He et al. (39) proposed a principled model attempting to address the mechanism of human-observer behavior. In particular, they presented evidence from the radiology literature to show that a human observer can be modeled as if he is an IO who uses information that exits the perception/cognitive systems. They termed this IO the equivalent IO (EIO). Different human observers have different amount of exiting data and thus different EIO performance. To measure the LR distributions of these EIOs, rationality must be enforced (39).
Advanced Model Observer Computational Techniques
Due to large data dimensionality found in medical imaging applications, significant computational difficulties arise in computing model observers. Barrett et al. called this problem the HO computation megalopinakophobia (40), i.e., fear of large matrices. For example, the image vector 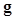 of a
of a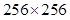 image is
image is 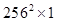 in dimension, and the dimension of its covariance matrix is
in dimension, and the dimension of its covariance matrix is 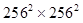 . Thus the computation of the HO involves inverting a
. Thus the computation of the HO involves inverting a 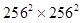 matrix. In addition to megalopinakophobia, the difficulty of computing an IO also comes from the often unknown PDFs of the image data. Even for phantoms defined by a set of parameters with known statistical distributions, the actual image statistics cannot be easily deduced from the sample images drawn from the distributions, nor can it be easily derived analytically.
matrix. In addition to megalopinakophobia, the difficulty of computing an IO also comes from the often unknown PDFs of the image data. Even for phantoms defined by a set of parameters with known statistical distributions, the actual image statistics cannot be easily deduced from the sample images drawn from the distributions, nor can it be easily derived analytically.
Despite the significant computational difficulties, the IO and HO computations are feasible for images obtained from parameterized phantoms or even real clinical images. There are two general types of techniques, Markov chain Monte Carlo (MCMC) and efficient channels. In the following subsections, these two types of techniques will be introduced first. The variance estimation and generalizability of model observers will then be discussed.
Computing an ideal observer using a Markov Chain Monte Carlo technique
Kupinski et al. proposed an MCMC technique to evaluate the non-linear IO test statistics for non-Gaussian images generated using a parameterized lumpy object model (41). In other words, Kupinski's MCMC allows LR computation in a BKS scenario. In particular, they formulated the LR in (4) as an expectation of the LR for the given known background (i.e., BKE case) over the posterior distribution of the background image 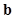 , i.e.,
, i.e.,
(20)
where 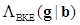 is the BKE LR and
is the BKE LR and 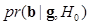 is the posterior distribution of
is the posterior distribution of 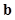 given
given 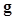 under
under 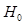 . Eqn. (20) can be estimated using the following Monte Carlo estimator,
. Eqn. (20) can be estimated using the following Monte Carlo estimator,
(21)
where 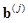 is the jth sample from
is the jth sample from 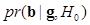 ,
, 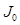 is used as a burn-in iteration to remove the unstable samples from the estimation, and J is the total number of samples used to estimate
is used as a burn-in iteration to remove the unstable samples from the estimation, and J is the total number of samples used to estimate 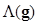 . Thus the difficulty in evaluating (21) resides in sampling from
. Thus the difficulty in evaluating (21) resides in sampling from 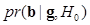 . Kupinski et al. proposed a Metropolis-Hastings MCMC algorithm that made this sampling possible. The basic idea is to first sample from the parameter space of the given background phantom b, create an ensemble of background phantoms, simulate the imaging process to obtain candidate background images from those phantoms, and then apply the Metropolis-Hastings algorithm to each candidate background image to decide whether to accept it as a sample from the posterior distribution. The accepted
. Kupinski et al. proposed a Metropolis-Hastings MCMC algorithm that made this sampling possible. The basic idea is to first sample from the parameter space of the given background phantom b, create an ensemble of background phantoms, simulate the imaging process to obtain candidate background images from those phantoms, and then apply the Metropolis-Hastings algorithm to each candidate background image to decide whether to accept it as a sample from the posterior distribution. The accepted 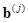 samples form a Markov chain for use in the estimation of LR given in (21). This process results in a good-sized set of accepted background images, which are sampled from the posterior distribution.
samples form a Markov chain for use in the estimation of LR given in (21). This process results in a good-sized set of accepted background images, which are sampled from the posterior distribution.
Park et al. added to this MCMC technique by providing a means to handle signal variability such as signal location and shape. In particular, Park formulated the LR in (20) as an expectation of the BKE LR over the posterior distribution of the image background as well as the distribution of the signal parameters. Park's formulation assumed independence between the signal and the background. A corresponding MCMC technique was developed (42).
Choosing efficient channels
To make the IO computation faster and more practical, Park et al. continued this line of research (28, 29). To further accelerate the computational speed and still approximate the IO or HO performance, Park et al. investigated the methods of choosing efficient channels for the CIO and CHO. For their investigation of efficient-channel methods, Park et al. developed another MCMC, which is an extension of the Kupinksi MCMC (43). In the Kupinski MCMC (40), a symmetric proposal density which enabled the use of Metropolis-Hastings MCMC technique, was developed to add/remove the original lump locations from the given lumpy background phantom b to/from the new background phantom, and also to randomly change each of the chosen original lump locations (i.e., if randomly chosen to be added to the new background) from the given lumpy background phantom via sampling from a Gaussian distribution with a fixed width. The Gaussian width was chosen so that the acceptance rate of the newly sampled lumpy background images was reasonable. The Park MCMC used this proposal density for generating lumpy background phantoms for forming its own Markov chain. However, the Park MCMC used an acceptance probability formula in the channelized data space in order to enable the calculation of the CIO rather than the IO, whereas the Kupinski MCMC used its acceptance probability formula in the image space. This way, the resulting Markov chain from the Park MCMC consisted of background images that were different from the Kupinski MCMC. The Park MCMC technique was instrumental in the subsequent investigation of a number of efficient-channel generating methods, which are described below.
We describe three sets of the most promising efficient channels as well as the importance of tuning channels properly. Examples of these channels are shown in Figure 2.
Laguerre-Gauss channels
Laguerre-Gauss (LG) functions make up an orthonormal basis for rotationally symmetric square-integrable functions (22). For an imaging system whose Hotelling template is rotationally symmetric, LG channels form a basis for the Hotelling template and hence are efficient for the Hotelling observer. Now the question is: what kind of image data will result in a rotationally symmetric HO template? The answer can be found in (30), from which we give a brief statement here: “The correlation structure of the background has no preferred orientation; thus it is rotationally symmetric. The signal is a smooth and rotationally symmetric function in a known location, and the measurement function of the imaging system is position independent and also rotationally symmetric. We infer from these characteristics of the signal, background, and imaging system that the template of the ideal linear observer will be a discretized version of a smooth and rotationally symmetric function located in the same place as the signal.”
Singular vectors (SV) channels
Park et al. investigated the use of singular vectors (SVs) of a linear pin-hole imaging system as efficient channels for the IO using non-Gaussian lumpy backgrounds and a Gaussian signal (29). They found that SV channels were more efficient than LG channels in terms of approximating both the nonlinear and linear IOs. However, since the SVs are only a basis for the imaging system, and contain no statistical information regarding the signal to be detected, a large number of SV channels are needed to approximate the IO performance compared to the LG channels as well as the other approach for choosing efficient channels described below (28).
Images of various channels. On top: examples of first 25 Laguerre-Gauss channels. Middle: examples of first 25 singular vector channels. Bottom: examples of first 25 PLS channels. Please refer to (28) for details of the system and image parameters for the generation of these channels. (reproduction of Fig. 2 in (28).)

An alternative to using the SVs of an imaging system as efficient channels is to use the SVs of the data covariance matrix computed from background images (44, 45). A main bottleneck of this approach when applied to realistic applications would be the number of sample images required to calculate a good estimate of data covariance, assuming one can overcome megalopinakophobia.
Partial least squares (PLS) channels
Note that the CIO with LG or SV channels are only applicable to rotationally symmetric signals or known imaging system matrices, respectively, and are only validated with respect to lumpy backgrounds. To overcome these difficulties and arrive at channels that may be applicable to real-life situations, Witten et al. [27] investigated a method using partial least squares (PLS) to compute efficient channels directly from the images. The PLS approach seeks to find a set of basis functions of the images that maximize the covariance between the data and the truth. Witten et al. found that PLS channels are more efficient than LG and SV channels in terms of both the number of channels and the ability to approximate performance.
Tuning channels
We use LG channels as an example. For LG channels to be efficient for the HO, it is important to tune the parameters of LG channels (the Gaussian width and the number of LG channels to be used). In our experience, the Gaussian width should be large enough to cover at least the signal spread and the optimal number of LG channels changes depending on the background and signal statistics. For example, the detection of a SKE Gaussian signal in white noise backgrounds can be done with one LG channel of the same width as that of the signal (i.e., the signal itself). If the background statistics change to have some spatial correlation, the number of LG channels has to increase to incorporate the background statistics information that affect the detection of the given signal (28).
CHO performance estimates and generality of model observers
Various statistical/computational methods have been developed to refine CHO methodologies. Here we give two examples. Wunderlich et. al (46-49) explored the potential to improve the estimation accuracy of CHO SNR2 by incorporating prior knowledge of the mean images into the estimation procedure. Uniformly minimum variance unbiased estimators of SNR2 were then proposed and shown to result in significantly lower bias and mean-square error than traditional estimators (48).
Generalizability of an observer, IO, HO or CHO, might be a desired feature for observer design. Because model observers are computed based on a surrogate population of images, exploration of the generalizability of a model observer might help to answer how model-observer performance results can be generalized to a more realistic population. Brankov's study explored the generalizability of a CHO which was implemented using a machine learning technique (50). Instead of using the sample mean and covariance matrices to compute the CHO template as in (7), Brankov trained the observer using supporting vector machine (SVM) to give scores that matched the human-observer scores given the same images. They found that the use of SVM enables good generalization over unseen data. In particular, Brankov trained the proposed observer and a traditional CHO trained using the same set of training images. He then applied the two observers to a set of testing images with different statistical properties from those of the training images (e.g. the testing images were reconstructed using different algorithms). Brankov showed that the proposed approach predicted human-observer performance on this set of testing images better than the traditional CHO.
Applications in Medical Imaging
We briefly survey a few applications of model observers in medical imaging research. Most of the following discussions will be focused on detection tasks or classification tasks. Please refer to Section II.A for a mathematical treatment of these tasks.
The ideal observer
Despite its robust theoretical foundations, the applications of the IO face two major challenges: computational burden and surrogate population/system selection. We have described the computational burden in Section III. The surrogate selection challenge refers to the fact that the IO is computed based on a representative population of images and a mathematical representation of an imaging system. The chosen image population and system representation are usually different from the ones used in reality. Since the exact PDFs of clinical images and the exact knowledge or modeling of clinical imaging systems are often not known or infeasible, how can we select their surrogates to obtain an IO whose performance is generalizable to the real images/systems? We do not have a principled answer for this question other than making the surrogates as realistic as computationally possible. This is a challenge that needs to be addressed by the image quality community in both theoretical and empirical manners. Here we briefly introduce a few studies in this endeavor.
The first example is the application of a rigorous mathematical model of real image backgrounds and noise. Abbey et al. applied the MCMC IO technique to the evaluation of breast CT imaging systems for breast cancer screening by formulating a binary object model that mimicked the attenuation coefficients of breast tissues (17). Two observations were made to facilitate the development of this object model. First they observed that tissue types in the breast parenchyma were essentially binary when ignoring skin, calcifications, etc. Second, the attenuation of cancerous tissue was relatively similar to that of glandular tissue. Then, Abbey et al. started with a parameterized object based on a Gaussian mixture using the sample mean and covariance of breast CT data for generating the distributions of adipose and glandular tissue textures. Then they binarized the parameterized objects based on the two assumptions described above. Both the parametric and resulting binary object models allowed the application of the MCMC IO technique for estimating classification task performance.
The second example used a realistically simulated database. He et al. applied the MCMC IO technique to compute the IO in a more realistic setting of a SPECT imaging system and a cardiac torso phantom (15). He et al. created a database for organ-only projection images using a discretely parameterized phantom. Thus instead of simulating the whole imaging process to sample from 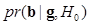 , they simply computed the image vector as a weighted summation of the organ-only images from the database. Despite the significant computational burden, this approach made it possible to estimate the IO performance using realistically simulated imaging systems and realistic object models. The readers may refer to (15) for a flow chart of implementing the MCMC IO technique.
, they simply computed the image vector as a weighted summation of the organ-only images from the database. Despite the significant computational burden, this approach made it possible to estimate the IO performance using realistically simulated imaging systems and realistic object models. The readers may refer to (15) for a flow chart of implementing the MCMC IO technique.
The third example is a direct derivation of an IO using a relatively simple object model. Graff and Myers (16) derived an IO for reconstructed MR images. This IO was firstly derived using reconstructed images for a single object in a SKE/BKE task where the noise was shown to follow non-central Chi distributions. Then the SKE/BKE IO was integrated over a population of objects to obtain an IO for a SKS task.
The above examples demonstrate the feasibility of IO optimization techniques. To make an actual impact, as with all other system design or optimization techniques, evaluation studies are a must. An essential evaluation study is to compare the technique of interest to an existing one. Case in point, comparison studies between systems optimized with the IO techniques and systems optimized with traditional techniques are needed. The comparisons should be done in terms of final human-observer performance, assuming the software systems are properly optimized. These comparison studies will provide crucial experimental evidence supporting the two-step optimization: the IO for hardware optimization and the human observers for software optimization. In addition, these comparison studies may also shine light on the challenge of surrogate selection.
Efficient channels for the IO and the HO estimation
The IO or HO computed with efficient channels are promising due to 1) their significantly reduced computational burden, 2) their potential for providing an unbiased estimate of the IO or HO performance, and 3) their potential applicability to clinical images. Most research on efficient channels has been done theoretically or using simulated images. Recently, Zhang et al. [33] investigated the feasibility of using PLS as a method of estimating efficient channels for digital breast tomosynthesis in computing the HO. Their preliminary results show the potential of PLS channels in extracting relevant statistical information for a binary detection task from more realistic simulated or clinical images.
The ideal linear observer or Hotelling observer for system optimization
The concept of the ideal linear observer or HO has been applied to task-based system optimization of several different modalities, such as ultrasound (51), MRI (16), SPECT scintimammography (52), CT imaging (53), and fluorescence-enhanced optical imaging systems (54). The basic idea is to linearize the IO, which can be done by 1) designing a modality specific object model, 2) deriving the system matrix, and 3) treating the system as a Gaussian stochastic process. For example, Graff and Myers formulated the IO for MR imaging (16). The “object” in MR imaging is the magnetic spins inside the physical object, and it is modeled as a function of the proton density, spin-lattice relaxation rate, and two spin-spin relaxation rates. The system model, or imaging process, is modeled as the Fourier transform of the product of spatio-temporal distribution of the spins and coil sensitivity. The noise in MR imaging is thermally generated and is modeled as zero-mean, equal variance normal distributions.
Simulation-based channelized Hotelling observer (CHO) studies
There is a large body of simulation-based CHO studies in nuclear medicine imaging. Such a study usually starts with realistically simulated images with signals (e.g. tumors) at known locations. Frequency-domain channels are then converted to those of the spatial domain and shifted such that the centers are aligned with the centroid of the signal on each image (Figure 1). Applying the spatial-domain channels using the formulas in (15) and (16) results in a channelized data vector v for each image. The vectors from a reasonably sized subset of the ensemble images are used for training of the CHO, i.e. computing a CHO template based on (7). The CHO template is then applied to the remaining set of the ensemble images for testing of the CHO, i.e., performance evaluation.
Gifford et al. studied the effects of a scatter-subtraction strategy on lesion detection in Hepatic SPECT imaging (55); Frey et al. studied the effects of various compensation methods on defect detection in myocardial perfusion SPECT imaging (56); Zeng et al. investigated a collimator design method using a channelized Hotelling trace on reconstructed images rather than projection images (57); Bal et al. used a CHO-based principle for automatic diagnosis of Parkinsonian disorders (58); Nuyts et al. investigated the performance of MAP reconstruction for hot lesion detection in whole-body PET/CT (59).
Direct computations of HOs from reconstructed images
Simulation-based CHO and HO studies are relatively resource demanding. Analytical approaches have been investigated to compute the HO or CHO from reconstructed images directly. The key is to find an analytical expression (even if it is only an approximation) for the CHO or HO SNR given different reconstruction algorithms and system settings. The core issue is to figure out ways to compute the mean and covariance matrices of the data. The computation of covariance matrices is particularly challenging. There are two directions in this endeavor. The first direction is for linear reconstruction algorithms such as filtered back projection (FBP). Wunderlich et. al. presented a method to compute the covariance matrices for images reconstructed using FBP for direct reconstruction from fan-beam data. In this work, Wunderlich et. al assumed Poisson noise model and a BKE task(46). For iterative algorithms, the computational difficulties reside in the non-linearity in most reconstruction algorithms as well as the non-stationary noise in most reconstructed images. The key to handle these difficulties is to make practical approximations on linearity of the reconstruction algorithm and local shift-invariance on the reconstructed images. Linearity approximation can be accomplished by using the 1st order Taylor expansion of a reconstructed image as a function of the projection image about the point of the mean projection image (60-64). Under the linearity assumption, a local impulse response function at each voxel can be derived, based on which a local covariance matrix can be computed (60, 65, 66). Further examples of computing covariance matrices for iterative algorithms can be found in (67, 68).
Frequency-domain HOs
The frequency-domain HO computation technique is also an analytical approach and there is increasing interest in its application to x-ray imaging. Siewerdsen et al. applied the frequency-domain HO to the assessment of various CT imaging systems, such as dual-energy CT imaging, tomosynthesis and cone-beam CT (69-72). In this approach, assuming the system noise was stationary, cascaded system analysis was used to compute various Fourier-domain system property metrics, such as the modulation transfer function (MTF), noise power spectrum (NPS), and noise equivalent quanta (NEQ), from which the SNR was calculated analytically. Some of the theoretical studies were then validated by human-observer studies demonstrating that the detectability derived this way correlated well with the performance of human observers (68).
Extensions of the CHO models
In addition to the traditional CHOs, advanced CHO models are investigated in recent literature. With the rapid growth of volumetric imaging, several authors have investigated multi-dimensional CHOs. Park et al. (73) developed a 3D projection (3Dp) HO and applied it to digital breast tomosynthesis. The key was to stack the ROIs of different angular projections to obtain concatenated vectors. The CHO was then computed from the concatenated vectors to incorporate spatial correlation between the angular projections. Several authors have investigated volumetric CHOs using 3D channels (74, 75). For example, Kinahan et al. used a set of 3D channels that are 3-dimensional extensions of the 2D channels shown in Figure 1. Specifically, each 3D channel formed a spherical shell in the 3D frequency domain (75). Chen et al. investigated a different principle for 3D CHO design. A 2D CHO was first computed for each slice and each view, the resulting test statistics from different slices and views were then integrated together to obtain the final test statistics (76). Platiša et al. discussed a principled 3-step approach for building an anthropomorphic observer (77): 1) start with the concept of an IO, 2) compare the IO performance to that of a human on a classification task; and 3) add constraints to the model to better predict human performance. They then designed multi-slice CHO models for the task of detecting 3D signals in 3D images as Step 1 (77). As part of Step 2, the performance of human observers in reading multi-slice images was recently presented (78).
Another interesting CHO extension is the LROC model observer (36, 79). It uses an affine local observer, e.g. a CHO, to compute a response at each location, and then the maximum of these responses is used as the global observer. This LROC model observer is used in the optimization of reconstruction algorithms in emission tomography (36, 79).
In light of the fast development of CHO models, we would like to draw the readers' attention to some fundamental issues. The CHO test statistics are often normally distributed due to the fact that each channelized data vector is a weighted summation of a large number of random variables, as seen in (15). When the test statistics are normally distributed with unequal variances, the resulting ROC curve may have a “hook”, which is considered unrealistic for human observers in the radiology literature (80). When the CHO test statistics have equal variances, the resulting ROC curve is not only convex but also symmetric. However, in a recent study, Samuelson observed that many ROC curves generated by radiologists using medical images follow a power-law shape, which is visibly non-symmetric (81). Based on these observations, in order to further refine the existing CHO models and also develop advanced CHO models, comparisons between the ROC curves of CHOs and those of human observers will also be beneficial in addition to comparing a CHO to human observers in terms of the AUC or SNR values.
Furthermore, in reading volumetric images, human observers integrate information obtained from multiple slices to make a decision. In addition, in tasks that involve search, human observers are uncertain about the locations of the signals. These phenomena may be related to two well-studied concepts in vision research: summation and uncertainty (82). We encourage interested readers to explore that direction for further development of anthropomorphic model observers.
Conclusions
In this paper, we reviewed the foundations, computational techniques, and applications of model observers in medical imaging research. Model-observer research has become an indispensable tool in the evaluation and optimization of imaging hardware and software systems in nuclear medicine, ultrasound imaging, x-ray imaging, and now MR imaging.
Model observers have strong theoretical foundations. The foundations of the optimal observers (IO and HO) are in statistical decision theory and linear discriminant analysis. The optimal observers are often used for system optimization. The anthropomorphic observers are designed to predict human-observer performance. The concept of anthropomorphic channels, which is probably the most important element in the development of anthropomorphic model observers, came from vision science. We believe that more should be borrowed from vision science for the future development of such observers.
The computation of model observers, especially the optimal ones, is mathematically difficult. We reviewed two types of techniques for addressing the computational difficulties: the MCMC and efficient-channel generating techniques. We believe that the efficient-channel approach has the potential to be used for more realistic image populations while significantly lowering the computational burden.
Finally, we reviewed a few applications of model observers in medical imaging research. These include the computation of the IO and HO for system optimization, efficient channels, frequency-domain HO computation in x-ray imaging, simulation-based CHO studies in nuclear medicine, direct HO and CHO computation for evaluating reconstructed images, and advanced CHO models for volumetric imaging.
Acknowledgements
We acknowledge the comments and suggestions from our colleagues, Dr. Brandon D. Gallas, Dr. Frank Samuelson, Dr. Christian Graff, Dr. Rongping Zeng, Dr. Adam Wunderlich, and Dr. Kyle J. Myers.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Barrett HH, Yao J, Rolland JP, Myers KJ. Model Observers for Assessment of Image Quality. Proceedings of the National Academy of Sciences of the United States of America. 1993;90:9758-9765
2. Barrett HH, Abbey CK, Clarkson E. Objective assessment of image quality. III. ROC metrics, ideal observers, and likelihood-generating functions. J Opt Soc Am A Opt Image Sci Vis. 1998;15:1520-1535
3. Barrett HH, Myers KJ. Foundations of Image Science. New York: Wiley & Sons. 2004
4. Dorfman DD, Berbaum KS, Metz CE. Receiver Operating Characteristic Rating Analysis - Generalization to the Population of Readers and Patients with the Jackknife Method. Investigative Radiology. 1992;27:723-731
5. Gallas BD. One-shot estimate of MRMC variance: AUC. Academic Radiology. 2006;13:353-362
6. Obuchowski NA, Rockette HE. Hypothesis-Testing of Diagnostic-Accuracy for Multiple Readers and Multiple Tests - An Anova Approach with Dependent Observations. Communications in Statistics-Simulation and Computation. 1995;24:285-308
7. Clarkson E, Kupinski MA, Barrett HH. A probabilistic model for the MRMC method, part 1: Theoretical development. Academic Radiology. 2006;13:1410-1421
8. Kupinski MA, Clarkson E, Barrett HH. A probabilistic model for the MRMC method, part 2: Validation and applications. Academic Radiology. 2006;13:1422-1430
9. Geisler WS. Ideal observer analysis. The visual neurosciences. Boston: MIT press. 2003:825-837
10. Geisler WS. Contributions of ideal observer theory to vision research. Vision Res. 2011;51:771-781
11. Geisler WS, Diehl RL. Bayesian natural selection and the evolution of perceptual systems. Philos Trans R Soc Lond B Biol Sci. 2002;357:419-448
12. Najemnik J, Geisler WS. Optimal eye movement strategies in visual search. Nature. 2005;434:387-391
13. Pelli DG, Palomares M, Majaj NJ. Crowding is unlike ordinary masking: Distinguishing feature integration from detection. Journal of Vision. 2004;4:1136-1169
14. Geisler WS, Kersten D. Illusions, perception and Bayes. Nature Neuroscience. 2002;5:508-510
15. He X, Caffo BS, Frey EC. Toward realistic and practical ideal observer (IO) estimation for the optimization of medical imaging systems. Ieee Transactions on Medical Imaging. 2008;27:1535-1543
16. Graff CG, Myers KJ. The ideal observer objective assessment metric for magnetic resonance imaging: application to signal detection tasks. Inf Process Med Imaging. 2011;22:760-71
17. Abbey CK, Boone JM. An ideal observer for a model of x-ray imaging in breast parenchymal tissue. Lecture Notes in Computer Science. 2008;5116:393-400
18. Beam CA, Layde PM, Sullivan DC. Variability in the interpretation of screening mammograms by US radiologists - Findings from a national sample. Archives of Internal Medicine. 1996;156:209-213
19. Park S. Spatial domain model observers for optimizing tomosynthesis. Reiser I, Glick SJ eds. Tomosynthesis Imaging: Taylor and Francis Books, Inc. 2013
20. Myers KJ, Barrett HH. Addition of A Channel Mechanism to the Ideal-Observer Model. Journal of the Optical Society of America A-Optics Image Science and Vision. 1987;4:2447-2457
21. Sachs MB, Nachmias J, Robson JG. Spatial-Frequency Channels in Human Vision. Journal of the Optical Society of America. 1971;61:1176 -
22. Gallas BD. Signal detection in lumpy backgrounds. University of Arizona. 2001
23. He X, Links JM, Frey EC. An investigation of the trade-off between the count level and image quality in myocardial perfusion SPECT using simulated images: the effects of statistical noise and object variability on defect detectability. Physics in Medicine and Biology. 2010;55:4949-4961
24. Abbey CK, Barrett HH. Human- and model-observer performance in ramp-spectrum noise: effects of regularization and object variability. Journal of the Optical Society of America A-Optics Image Science and Vision. 2001;18:473-488
25. Burgess AE, Li X, Abbey CK. Visual signal detectability with two noise components: Anomalous masking effects. Journal of the Optical Society of America A-Optics Image Science and Vision. 1997;14:2420-2442
26. Zhang Y, Pham BT, Eckstein MP. The effect of nonlinear human visual system components on performance of a channelized hotelling observer in structured backgrounds. Ieee Transactions on Medical Imaging. 2006;25:1348-1362
27. He X, Frey EC, Links JM, Gilland KL, Segars WP, Tsui BMW. A mathematical observer study for the evaluation and optimization of compensation methods for myocardial SPECT using a phantom population that realistically models patient variability. Ieee Transactions on Nuclear Science. 2004;51:218-224
28. Witten JM, Park S, Myers KJ. Partial Least Squares: A Method to Estimate Efficient Channels for the Ideal Observers. Ieee Transactions on Medical Imaging. 2010;29:1050-1058
29. Park S, Witten JM, Myers KJ. Singular Vectors of a Linear Imaging System as Efficient Channels for the Bayesian Ideal Observer. Ieee Transactions on Medical Imaging. 2009;28:657-668
30. Gallas BD, Barrett HH. Validating the use of channels to estimate the ideal linear observer. Journal of the Optical Society of America A-Optics Image Science and Vision. 2003;20:1725-1738
31. Zhang Y, Pham BT, Eckstein MP. Evaluation of internal noise methods for Hotelling observer models. Medical Physics. 2007;34:3312-3322
32. Park S, Badano A, Gallas BD, Myers KJ. Incorporating Human Contrast Sensitivity in Model Observers for Detection Tasks. Ieee Transactions on Medical Imaging. 2009;28:339-347
33. He X, Gallas BD, Frey EC. Three-class ROC analysis--toward a general decision theoretic solution. IEEE Trans Med Imaging. 2010;29:206-215
34. Clarkson E, Shen FF. Fisher information and surrogate figures of merit for the task-based assessment of image quality. Journal of the Optical Society of America A-Optics Image Science and Vision. 2010;27:2313-2326
35. Clarkson E. Estimation receiver operating characteristic curve and ideal observers for combined detection/estimation tasks. Journal of the Optical Society of America A-Optics Image Science and Vision. 2007;24:B91-B98
36. Khurd P, Gindi G. Rapid computation of LROC figures of merit using numerical observers (for SPECT/PET reconstruction). Ieee Transactions on Nuclear Science. 2005;52:618-626
37. Chakraborty DP. Recent advances in observer performance methodology: Jackknife free-response ROC (JAFROC). Radiation Protection Dosimetry. 2005;114:26-31
38. Chakraborty DP, Berbaum KS. Observer studies involving detection and localization: Modeling, analysis, and validation. Medical Physics. 2004;31:2313-2330
39. He X, Samuelson F, Gallas BD, Sahiner B, Myers K. The equivalence between a human observer and an ideal observer. SPIE Medical Imaging. 2013
40. Barrett HH, Myers KJ, Gallas BD, Clarkson E, Zhang H. Megalopinakophobia: its symptoms and cures. Antonuk LE, Yaffe MJ, eds. 2012:299-307
41. Kupinski MA, Hoppin JW, Clarkson E, Barrett HH. Ideal-observer computation in medical imaging with use of Markov-chain Monte Carlo techniques. Journal of the Optical Society of America A-Optics Image Science and Vision. 2003;20:430-438
42. Park S, Kupinski MA, Clarkson E, Barrett HH. Ideal-observer performance under signal and background uncertainty. Information Processing in Medical Imaging, Proceedings. 2003;2732:342-353
43. Park S, Barrett HH, Clarkson E, Kupinski MA, Myers KJ. Channelized-ideal observer using Laguerre-Gauss channels in detection tasks involving non-Gaussian distributed lumpy backgrounds and a Gaussian signal. Journal of the Optical Society of America A-Optics Image Science and Vision. 2007;24:B136-B150
44. Kupinski MA, Clarkson E. Extending the channelized Hotelling observer to account for signal uncertainty and estimation tasks. SPIE Medical Imaging. 2013;5749:183-190
45. Palit R, Kupinski MA, Barrett HH. et al. Singular Value decomposition of pinhole SPECT systems. 2009.
46. Wunderlich A, Noo F. Image covariance and lesion detectability in direct fan-beam x-ray computed tomography. Physics in Medicine and Biology. 2008;53:2471-2493
47. Wunderlich A, Noo F. On Efficient Assessment of Image-Quality Metrics Based on Linear Model Observers. Ieee Transactions on Nuclear Science. 2012;59:568-578
48. Wunderlich A, Noo F. Estimation of Channelized Hotelling Observer Performance With Known Class Means or Known Difference of Class Means. Ieee Transactions on Medical Imaging. 2009;28:1198-1207
49. Wunderlich A, Noo F. New Theoretical Results on Channelized Hotelling Observer Performance Estimation With Known Difference of Class Means. Ieee Transactions on Nuclear Science. 2013;60:182
50. Brankov JG, Yang YY, Wei LY, El Naqa I, Wernick MN. Learning a Channelized Observer for Image Quality Assessment. Ieee Transactions on Medical Imaging. 2009;28:991-999
51. Abbey CK, Nguyen NQ, Insana MF. Optimal Beamforming in Ultrasound Using the Ideal Observer. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2010;57:1782-1796
52. La Riviere PJ, Pan X, Penney BC. Ideal-observer analysis of lesion detectability in planar, conventional SPECT, and dedicated SPECT scintimammography using effective multi-dimensional smoothing. Ieee Transactions on Nuclear Science. 1998;45:1273-1279
53. Sidky EY, Pan XC. In-depth analysis of cone-beam CT image reconstruction by ideal observer performance on a detection task. Nuclear Science Symposium Conference Record, NSS '08. IEEE. 2008
54. Sahu AK, Joshi A, Kupinski MA, Sevick-Muraca EM. Assessment of a fluorescence-enhanced optical imaging system using the Hotelling observer. Optics Express. 2006;14:7642-7660
55. Gifford HC, King MA, de Vries DJ, Soares EJ. Channelized hotelling and human observer correlation for lesion detection in hepatic SPECT imaging. Journal of Nuclear Medicine. 2000;41:514-521
56. Frey EC, Gilland KL, Tsui BMW. Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT. Ieee Transactions on Medical Imaging. 2002;21:1040-1050
57. Zeng GSL, Gullberg GT. A channelized-hotelling-trace collimator design method based on reconstruction rather than projections. Ieee Transactions on Nuclear Science. 2002;49:2155-2158
58. Bal H, Bal G, Acton PD. Diagnosis of Parkinsonian disorders using a channelized Hotelling observer model: Proof of principle. Medical Physics. 2007;34:3987-3995
59. Nuyts J, Michel C, Brepoels L. et al. Performance of MAP Reconstruction for Hot Lesion Detection in Whole-Body PET/CT: An Evaluation With Human and Numerical Observers. Ieee Transactions on Medical Imaging. 2009;28:67-73
60. Bonetto P, Qi JY, Leahy RM. Covariance approximation for fast and accurate computation of channelized Hotelling observer statistics. Ieee Transactions on Nuclear Science. 2000;47:1567-1572
61. Qi JY, Leahy RM. A theoretical study of the contrast recovery and variance of MAP reconstructions from PET data. Ieee Transactions on Medical Imaging. 1999;18:293-305
62. Fessler JA. Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): Applications to tomography. Ieee Transactions on Image Processing. 1996;5:493-506
63. Barrett HH, Wilson DW, Tsui BMW. Noise Properties of the Em Algorithm.1. Theory. Physics in Medicine and Biology. 1994;39:833-846
64. Soares EJ, Byrne CL, Glick SJ. Noise characterization of block-iterative reconstruction algorithms: I. Theory. Ieee Transactions on Medical Imaging. 2000;19:261-270
65. Fessler JA, Rogers WL. Spatial resolution properties of penalized-likelihood image reconstruction: Space-invariant tomographs. Ieee Transactions on Image Processing. 1996;5:1346-1358
66. Qi JY, Leahy RM. Resolution and noise properties of MAP reconstruction for fully 3-D PET. Ieee Transactions on Medical Imaging. 2000;19:493-506
67. Li YS. Noise propagation for iterative penalized-likelihood image reconstruction based on Fisher information. Physics in Medicine and Biology. 2011;56:1083-1103
68. Stayman JW, Fessler JA. Efficient calculation of resolution and covariance for penalized-likelihood reconstruction in fully 3-D SPECT. Ieee Transactions on Medical Imaging. 2004;23:1543-1556
69. Gang GJ, Lee J, Stayman JW. et al. Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance. Medical Physics. 2011;38:1754-1768
70. Gang GJ, Tward DJ, Lee J, Siewerdsen JH. Anatomical background and generalized detectability in tomosynthesis and cone-beam CT. Medical Physics. 2010;37:1948-1965
71. Prakash P, Zbijewski W, Gang GJ. et al. Task-based modeling and optimization of a cone-beam CT scanner for musculoskeletal imaging. Medical Physics. 2011;38:5612-5629
72. Richard S, Siewerdsen JH, Tward DJ. NEQ and Task in Dual-Energy Imaging: From Cascaded Systems Analysis to Human Observer Performance. Proc.of SPIE 6913 ed. 2008
73. Park S, Jennings R, Liu HM, Badano A, Myers K. A statistical, task-based evaluation method for three-dimensional x-ray breast imaging systems using variable-background phantoms. Medical Physics. 2010;37:6253-6270
74. Lartizien C, Kinahan PE, Comtat C. Volumetric model and human observer comparisons of tumor detection for whole-body positron emission tomography. Academic Radiology. 2004;11:637-648
75. Kim JS, Kinahan PE, Lartizien C, Comtat C, Lewellen TK. A comparison of planar versus volumetric numerical observers for detection task performance in whole-body PET imaging. Ieee Transactions on Nuclear Science. 2004;51:34-40
76. Chen M, Bowsher JE, Baydush AH, Gilland KL, Delong DM, Jaszczak RJ. Using the Hotelling observer on multislice and multiview simulated SPECT myocardial images. Ieee Transactions on Nuclear Science. 2002;49:661-667
77. Platisa L, Goossens B, Vansteenkiste E. et al. Channelized Hotelling observers for the assessment of volumetric imaging data sets. Journal of the Optical Society of America A-Optics Image Science and Vision. 2011;28:1145-1163
78. Platisa L, Kumcu A, Platisa M. et al. Volumetric detection tasks with varying complexity: human observer performance. SPIE Medical Imaging, 8318 ed. 2012
79. Khurd P, Gindi G. Fast LROC analysis of Bayesian reconstructed emission tomographic images using model observers. Physics in Medicine and Biology. 2005;50:1519-1532
80. Pesce LL, Metz CE, Berbaum KS. On the convexity of ROC curves estimated from radiological test results. Acad Radiol. 2010;17:960-968
81. Samuelson F. The Single-Parameter Power Law for Modeling Data from Observer Experiments in Medical Imaging. Medical Image Perception Conference XIV, Dublin, Ireland. 2011
82. Pelli DG. Uncertainty explains many aspects of visual contrast detection and discrimination. J Opt Soc Am A. 1985;2:1508-1532
Author contact
![]() Corresponding author: xin.hehhs.gov
Corresponding author: xin.hehhs.gov
 Global reach, higher impact
Global reach, higher impact