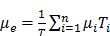13.3
Impact Factor
Theranostics 2017; 7(18):4551-4565. doi:10.7150/thno.19782 This issue Cite
Review
Quantitative Imaging for Targeted Radionuclide Therapy Dosimetry - Technical Review
1. Biomedical Imaging Laboratory, Department of Electrical and Computer Engineering, Faculty of Science and Technology, University of Macau, Macau SAR, China;
2. Dept of Radiology and Nuclear medicine, Ghent University, De Pintelaan 185 9000 Gent, Belgium;
3. AZ Maria Middelares, Buiten-Ring-Sint-Denijs 30, 9000 Gent, Belgium;
4. Dept of Nuclear Medicine, UZ Ghent-Ghent University, St-Pietersnieuwstraat 41, 9000 Gent, Belgium;
5. MEDISIP-ELIS-IBITECH-IMEC, Ghent University, St-Pietersnieuwstraat 41, 9000 Gent, Belgium;
6. Faculty of Health Sciences, University of Macau, Macau SAR, China.
Received 2017-2-23; Accepted 2017-7-25; Published 2017-10-13
Abstract
Targeted radionuclide therapy (TRT) is a promising technique for cancer therapy. However, in order to deliver the required dose to the tumor, minimize potential toxicity in normal organs, as well as monitor therapeutic effects, it is important to assess the individualized internal dosimetry based on patient-specific data. Advanced imaging techniques, especially radionuclide imaging, can be used to determine the spatial distribution of administered tracers for calculating the organ-absorbed dose. While planar scintigraphy is still the mainstream imaging method, SPECT, PET and bremsstrahlung imaging have promising properties to improve accuracy in quantification. This article reviews the basic principles of TRT and discusses the latest development in radionuclide imaging techniques for different theranostic agents, with emphasis on their potential to improve personalized TRT dosimetry.
Keywords: Nuclear medicine imaging, targeted radionuclide therapy, internal dosimetry, theranostic agents.
Introduction
Targeted radionuclide therapy (TRT) plays an increasingly important role for treating a range of cancers. The therapeutic agent is administered to the patients via different methods, i.e., intravenous injection [1-3], oral uptake [4], loco-regional, arterial [5] or direct intratumoral injection. The aim of TRT is to deliver a lethal dose of radiation to tumors from internal sources by targeting their specific molecular or functional targets with agents. The local dose is delivered directly by short ranged beta, Auger or alpha particles [6], or indirectly via the “bystander” effect [7]. Thus, compared to conventional chemotherapy or external radiotherapy, it has the potential to deliver therapeutic radiation more specifically to cancerous cells in a way that minimizes toxicity to surrounding normal tissues [8]. Iodine based thyroid therapy is a classic example of TRT. During the last years, there has been a significant growth of TRT due to a number of new isotopes and radiopharmaceuticals for the treatment of metastatic bone pain, neuroendocrine and other solid tumors, mainly in the liver.
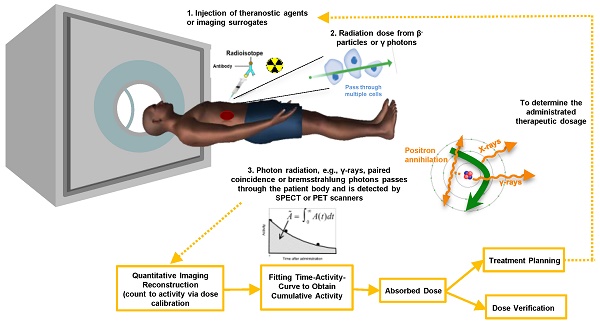
The distribution of the radionuclides is variable among patients [9]. Therefore, clinical practitioners would like to have a priori-knowledge of the biodistribution and washout of TRT agents before TRT. This information enables optimization of the therapeutic efficacy by adjusting the administered dose to each patient, and can be obtained non-invasively by single or sequential nuclear medicine scans, e.g., planar and emission computed tomography (ECT) or combined with blood sampling if necessary. Quantitative images at different time points allow fitting of time activity curves for the targeted organs and tumors. From the integration of these time-activity curves one can obtain the cumulative activity and further convert it to the absorbed dose, which can help pre-treatment planning or post-therapy dose verification. The whole dosimetry estimation procedure is shown in Figure 1.
Despite the growing recognition of personalized TRT dosimetry based on the actual agent biodistribution for each patient, the “one-dose-fits-all” or activity per unit body weight approach is still the common practice in TRT. For example, a fixed high activity of 2.8-7.4 GBq of I-131 is often used to treat thyroid cancer [10]. However, >10% of patients received blood doses exceeding the dose limit that would lead to myelotoxicity [11], and 80% of lesions investigated received a dose deposition of <80 Gy [12]. These studies suggest that fixed activity administrations either give low amounts of therapeutic agent to cautiously avoid deleterious effects in normal tissues with a loss of therapeutic efficacy to tumors, or potentially harm normal tissues by overexposure. Moreover, Strigari et al. indicated that personalized treatment planning would increase the survival rate and improve clinical efficacy by showing strong correlations among received absorbed dose, treatment response and toxicity, based on a review of 79 studies [13].
Till now, the accuracy for individualized organ dose assessment is still limited by: (i) uncertainties in activity quantification due to limitations in the imaging systems, with insufficient or inaccurate physics modeling in the quantitative imaging process [14]; and (ii) post-processing errors in sequential images including segmentation, registration, curve fitting for cumulative activity estimation, and methods for dose estimation based on the cumulative activity. Therefore, there is an increasing necessity for developing accurate, precise and streamlined methods for individualized patient dosimetric estimation for the future of TRT. The purpose of this article is to give an up-to-date and comprehensive overview of methods in TRT dosimetry, i.e., advanced quantitative imaging technologies for activity estimation, with emphasis on the inherent theranostic characteristics of TRT agents, since the review from Erdi et al. [15], Bardiès et al. [16] and Ljungberg et al. [17, 18] which focused more on conventional radionuclide imaging methods.
Radiopharmaceuticals for radionuclide therapy
The concept of theranostics was launched in 2002 by Funkhouser and refers to a material that possesses both therapeutic and diagnostic capabilities [19]. Thus, it delivers therapeutic drugs and diagnostic imaging agents at the same time with the same dose, which is the case for TRT tracers. However, many TRT radionuclides are not optimal for imaging as they either do not have simultaneous gamma/positron emission, the abundance of gamma photons/positrons is too low, or the energy of the photons is too high. The most frequently used TRT isotopes in current clinical routine are I-131 for thyroid therapy, Y-90 for radio-embolization, Lu-177 for neuroendocrine tumors and Ra-223 for bone tumors. An additional notable TRT radionuclide is Ho-166, which is a combined beta-gamma emitter, CT agent and an ideal paramagnetic MR contrast agent. These properties made Ho-166 labeled poly (L-lactic acid) microsphere (Ho-166-PLLA-MS) a promising agent for radio-embolization (RE) of hepatic tumors in selective internal radiation therapy (SIRT) [20, 21]. However, its short half-life of 26.8 h indicates that each dose will require separate neutron irradiation and a short timeline to get the dose from the reactor to the patient [22].
Flowchart and the potential error sources for imaging-based TRT dosimetry.
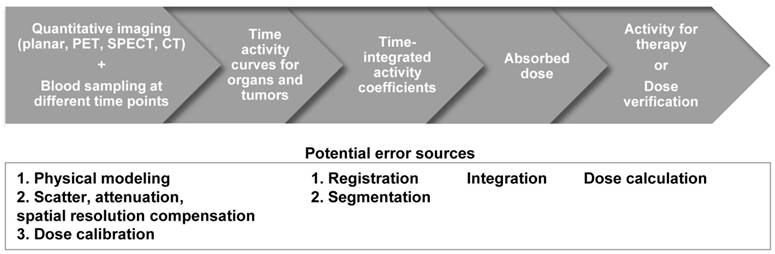
Although direct imaging of these radionuclides is possible via PET or a conventional gamma camera with the appropriate choice of collimator, energy window and detectors, the image quality is usually inferior to the quality of current F-18 based PET and Tc-99m based SPECT studies, and therefore quantitation is challenging. Alternatively, the distribution of these tracers can be estimated indirectly for planning treatment with the use of theranostic 'surrogate' pairs for imaging and therapy. This refers to the same biomolecule labeled with 2 different radio-isotopes, possessing similar biological and chemical characteristics. However, one is for therapy while the other one is more effective with regards to imaging. Since surrogate imaging isotopes may have different half-lives as compared to their therapeutic partners, it is necessary to apply decay corrections on the pharmacokinetic models predicted from a static distribution of the surrogate imaging isotope [23]. The concept of direct and indirect imaging is illustrated in Figure 2. Common TRT radiopharmaceuticals, their imaging surrogates and their reported organ absorbed doses in different patient studies are listed in Table 1.
Advanced techniques for imaging surrogate/theranostic isotopes
Most of the available dose calculation software needs the input of the cumulative activity in different organs. In order to get the cumulative activity, one needs to obtain activity distributions for different organs at different time points. Functional radionuclide imaging techniques such as planar, SPECT, bremsstrahlung and PET imaging can serve for this purpose. The accuracy of TRT dosimetry is therefore highly dependent on the quantitative accuracy of the imaging techniques. Each of the different imaging techniques are described in detail below.
Absorbed doses to critical organs and tumors for various TRT agents.
| Therapeutic radionuclide | Probe | Ref | Radionuclide for Dosimetry | Mean Absorbed Dose for Critical Organs / Tumors (mGy/MBq or Gy) | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I-131 | Iodine | [24]* | I-124 | Bone marrow | Liver | Kidneys | Heart | Lungs | Tumor | ||||||||||||||||||||||
| rhTSH | 0.07-0.33 | 0.11-0.4 | 0.11-0.44 | 0.11-0.46 | 0.1-0.44 | 0.05-21 | |||||||||||||||||||||||||
| THW | 0.08-0.22 | 0.19-0.24 | 0.17-0.32 | 0.1-0.33 | 0.11-0.66 | 0.12-82 | |||||||||||||||||||||||||
| Tositumomab | [25] | I-131 | Bone marrow | ||||||||||||||||||||||||||||
| Imaging | 0.57-1.44 Gy | ||||||||||||||||||||||||||||||
| Blood sampling | 0.40-1.55 Gy | ||||||||||||||||||||||||||||||
| MIBG | [26] | I-131 | Adrenals | Spleen | Salivary glands | Bladder | Heart | ||||||||||||||||||||||||
| 0.17 | 0.49 | 0.23 | 0.59 | 0.072 | |||||||||||||||||||||||||||
| Kidneys | Liver | Lungs | Pancreas | ||||||||||||||||||||||||||||
| 0.12 | 0.83 | 0.19 | 0.10 | ||||||||||||||||||||||||||||
| Y-90 | Microspheres | [27] | Y-90 | Liver | 18.3±10.3 | Tumor | 148.1±92.1 | ||||||||||||||||||||||||
| Zevalin | Kidneys | Liver | Spleen | Lungs | Bone marrow | Tumor | |||||||||||||||||||||||||
| [28] | Zr-89 | N/A | 3.2 ± 1.8 | 2.9 ± 0.7 | N/A | 0.52 ± 0.04 | 8.6-28.6 | ||||||||||||||||||||||||
| [29] | In-111 | 0.01-0.65 | 2.2-11.0 | 3.50-26.0 | 1.30-4.30 | 0.26-1.10 | N/A | ||||||||||||||||||||||||
| Y-90 | 0.0-0.3 | 2.9-8.1 | 1.8-20.0 | 1.2-3.4 | 0.6-1.8 | N/A | |||||||||||||||||||||||||
| DOTA octreotide | Kidneys | Liver | Spleen | Bone marrow | Tumor | ||||||||||||||||||||||||||
| [30] | Y-86 | 2.73 ± 1.41 | 0.66 ± 1.5 | 2.32 ± 1.97 | 0.49 ± 0.002 | 32.1-195.8 | |||||||||||||||||||||||||
| [31] | Y-86 | 1.71 ± 0.89 | 0.72 ± 0.40 | 2.19 ± 1.11 | 0.06 ± 0.02 | 2.1-29.5 | |||||||||||||||||||||||||
| [32] | In-111 | 3.9 ± 1.9 | 0.72 ± 0.57 | 7.62 ± 6.30 | 0.6 ± 0.2 | 1.4-31 | |||||||||||||||||||||||||
| [33] | In-111 | 2.84 ±0 .64 | 0.92 ± 0.35 | 6.57 ± 5.25 | 0.17 ± 0.02 | 2.4-41.7 | |||||||||||||||||||||||||
| In-111 | DPTA octreotide | [34, 35] | In-111 | 0.52 ± 0.24 | 0.065 ± 0.01 | 0.34 ± 0.16 | 0.03 ± 0.01 | 0.72-6.8 | |||||||||||||||||||||||
| Lu-177 | DOTA octreotide | [34] | Lu-177 | 1.65 ± 0.47 | 0.21 ± 0.07 | 2.15 ± 0.39 | 0.07 ± 0.004 | 3.9-37.9 | |||||||||||||||||||||||
| PSMA | [36] | Lu-177 | Parotid glands | Kidneys | Bone marrow | Tumor | Bone metastases | Lymph node metastases | |||||||||||||||||||||||
| 1.3±2.3 | 0.8±0.4 | 0.07 ± 0.004 | 3.3±14 | 0.03 ± 0.01 | 4.0±20 | ||||||||||||||||||||||||||
| Ho-166 | DOTMP | [37] | Ho-166 | Kidneys | Bone marrow | Bone surfaces | Bladder | ||||||||||||||||||||||||
| 0.045±0.005 | 0.52 ± 0.22 | 0.78±0.30 | 0.84 ±0.17 | ||||||||||||||||||||||||||||
| Microspheres | [38] | Ho-166 | Liver | Tumor | |||||||||||||||||||||||||||
| SPECT | 7.7-54.3 Gy | 9.1-68.2 Gy | |||||||||||||||||||||||||||||
| MR | 13.2-64.9 Gy | 14.8-75.4 Gy | |||||||||||||||||||||||||||||
| Sm-153 | EDTMP | [39] | Sm-153 | Bone marrow | 0.3-2.1 | Bone surface | 2.3-14.3 | ||||||||||||||||||||||||
| Sr-89 | Chloride | [40] | Sr-85 | Skeletal metastases | 215±65.19 | ||||||||||||||||||||||||||
| Re-188 | HEDP | [41] | Re-188 | Bone metastases | Bone marrow | Kidneys | Bladder | ||||||||||||||||||||||||
| 3.83±2.01 | 0.61±0.21 | 0.71±0.22 | 0.99±0.18 | ||||||||||||||||||||||||||||
* Patients with metastatic differentiated thyroid cancer were injected with THW or rhTSH prior to I-131 administration. THW = thyroid stimulating hormone withdrawal; rhTSH = recombinant human thyroid-stimulating hormone.
MIBG=Metaiodobenzylguanidine; PSMA=Prostate-specific membrane antigen; HEDP=Hydroxyethyledine diphosphonate; EDTMP=Ethylenediamine tetramethylene phosphonate; DOTMP = 1, 4, 7, 10 tetraazacyclododecane-1, 4, 7, 10-tetramethylene-phosphonate
The concept of direct and indirect imaging methods for TRT agents.
Planar scintigraphy
Traditional Conventional Planar (CPlanar) method was first proposed by Thomas et al., which was based on calculating the geometric-mean (GM) of two conjugate counting views in combination with the effective attenuation correction (AC) [42]. This method usually requires drawing the region-of-interest (ROI) on the anterior and posterior whole-body images. The activity A in the ROI is given by:
;
Where IA and IB are the counts in the ROI on the anterior and posterior images respectively, µe is the effective attenuation coefficient and can be calculated by the average of all attenuation coefficients in each region, T is the body thickness, C is the calibration factor and i is the pixel index. This method is theoretically independent of the source depth and gives a reasonable dose estimate for large organs without position overlap and background activity. The main limitation of this method is the organ-organ or organ-background overlap in the projections, which may lead to errors in the activity estimation for the organs-of-interest [43]. Sjogreen et al. showed that if the attenuation map derived from integrated CT along the anterior-posterior direction was used to aid the volume definition and to perform background and overlapping organs correction, the activity estimation errors for major organs in planar imaging could be reduced to -21%. For spherical tumors with diameters of 3.6 or 2.9 cm, the activity might be underestimated by -6% to -47%, varying with tumor location [44].
Multiple hybrid methods were developed to improve the quantitative accuracy for planar imaging with accurate modelling of the physical factors, e.g., Quantitative Planar (QPlanar) [45] and Extended QPlanar (EQPlanar) [46] methods. EQPlanar combines the advantages of fast acquisition in conventional planar imaging with SPECT by manually delineating the 3D volumes-of-interest (VOIs) from one time point SPECT to partially solve the organs overlap problem.
Despite the fact that 3D voxel-based dosimetry cannot be achieved by the planar method, it is still the mainstream dosimetric method for TRT as it takes just a few minutes for acquisition and is less computationally intensive. It can be implemented relatively easily on modern dual-head gamma cameras.
Quantitative SPECT
The use of SPECT provides 3D spatial information and solves the problem of organ overlap and reduced contrast caused by background activity in planar imaging. This is an essential step in enabling 3D voxel-based dosimetry. Moreover, modern dual modality SPECT/CT scanners provide an improved attenuation map from CT for performing AC in SPECT reconstruction. The anatomical information from CT also improves organ delineation in TRT.
In a comprehensive quantitative SPECT method (QSPECT) proposed by He et al.[47], scatter compensation (SC) was performed using effective source scatter estimation (ESSE) [48] which requires effective scatter source kernel and scatter attenuation coefficient kernel convolutions for each projection. Partial volume compensation (PVC) was done using the perturbation based geometric transfer matrix (pGTM) [49]. The collimator-detector-response (CDR) compensation was estimated by Monte Carlo simulations (MCS) based on the collimator parameters and CT was used for AC. Accuracy within 10% could be achieved for all organs in the radiology support device (RSD) torso phantom while only the lungs had a higher error (11%). He et al. later showed that the SPECT acquisition time could be shortened by a factor of at least 2 with a change in mean error of <1% [50]. When the scan time was reduced to 1.5 min, the accuracy and precision in hot and large organs were still acceptable. Even if the scanning time can be shortened, two bed positions are still required to cover the whole torso for quantification, increasing difficulties in designing the scanning protocol. However, 1 bed position could be enough if only critical organs are of interest in some applications, further reducing the acquisition time.
Shcherbinin et al. applied the interpolated analytical photon distribution (APDI) [51] method which uses the Klein-Nishina cross-section to analytically calculate the scatter distribution in the forward projection step of the iterative ordered subsets expectation maximization (OS-EM) reconstruction [52], shortening the computation time compared with the MCS-based SC method. Errors of activity estimation were within 10% for Tc-99m, In-111, I-123 and I-131.
Dewaraja et al. developed a regularized reconstruction method to reduce the edge artifacts caused by CDR compensation after large update numbers [53] and improve the accuracy of activity distribution within the targets [54]. The penalized-likelihood function utilized the anatomical information provided by the CT images (PL-CT) and was added to the reconstruction process after certain updates of OS-EM. In both simulation and phantom studies with uniform activity distribution, PL-CT outperformed both the regularized reconstruction without CT and the routine OS-EM reconstruction in visual assessment, image profile and target activity distribution.
Since gamma cameras are mostly optimized for imaging low and mono-energetic isotopes, different problems may occur when imaging the therapeutic isotopes emitting high energy gamma rays or particles, e.g., collimator penetration, contamination from higher energy peaks and secondary X-rays. For example, I-131 emits 364 keV photons and a large amount of penetration occurs when used in combination with medium energy collimators. Dedicated high-energy collimators can be used to reduce penetration but this typically results in poor spatial resolution. Some TRT isotopes not only have low energy gammas but also small fractions of high-energy photons. As the collimator septa are designed for low energy peaks, a relatively large fraction of high-energy photons will penetrate the collimator. Also, the ones that scatter in the patients or collimator/detector can still end up in the energy window of the main photopeak. Even if these photons pass through both collimator and detector, they can still backscatter from the remaining parts of the gamma camera to the detector.
In addition, the attenuation and scatter corrections also need to be adapted for TRT isotopes. For example, some isotopes have two low energy peaks for imaging but each requires a different attenuation factor. For AC, one can simply discard photons from one of the energy windows, which would lead to a huge loss of information especially for isotopes whose two peaks have similar abundance, e.g., In-111 and Lu-177. Another approach would be to acquire photons from 2 peaks separately or enable list-mode acquisition, with 2 reconstructions followed by combination of the two images. However, this approach suffers from increased storage, acquisition or computational time. One way to solve this problem is to use an effective attenuation coefficient that regards the photopeaks as a single photon energy, which could make maximal use of the available information with no extra computational burden [55]. Model-based SC, such as ESSE, estimates scatter using an effective scatter source [48] by pre-calculating the blurring kernels from MCS. This is superior to energy window-based SC for clinical TRT, with reasonable reconstruction time.
The latest MIRD pamphlet presents a set of guidelines for data acquisition protocols and image reconstruction techniques recommended for quantitative Lu-177 SPECT [56]. Medium energy collimators are recommended for their good signal-to-noise ratio (SNR) due to reduced septal penetration of high-energy photons. An energy window of 15%-20% centered on the 208 keV photopeak is suggested for acquisition. Occasionally the 113 keV peak can be acquired as well if counts collected in the 208 keV window are insufficient. However, self-scatter of 113 keV photons and down-scatter of 208 keV photons into this 113 keV energy window should be taken into consideration, and triple energy window (TEW) SC method is a potential solution. He et al. applied their QSPECT method for Lu-177 in a physical phantom study [57]. TEW was used to generate projection data including a 20% energy window for photopeaks of 208 keV, 113 keV and the combination of both peaks. Errors were <3.2% for all organs using the 208 keV energy window, up to 40% using only the 113 keV energy window, and up to 14% for the combined photopeaks.
Bremsstrahlung imaging
When imaging theranostic isotopes, e.g., Y-90, Sr-89 and Ho-166, it is important to mention the presence of secondary radiation not directly generated from gamma decay itself. The electrons emitted from β- decay undergo several interactions with the surrounding tissue before being stopped. By interacting with other charged particles they can generate bremsstrahlung photons (similar to x-ray generation in an X-ray tube). This leads to a continuous spectrum of X-ray with a maximum energy equal to the maximum energy of the emitted electrons. A typical spectrum is shown in Figure 3. The distance travelled from the point of emission before bremsstrahlung is inversely related to the energy of the emitted X-ray. The amount of X-rays generated depends on the material (more in dense materials like bone). Typically only a few percent of emitted electrons will generate secondary X-rays. For example, about 2-4% of Y-90 decays will lead to bremsstrahlung X-ray generation.
The process for Y-90 radionuclide therapy and bremsstrahlung imaging for Y-90 dosimetry with a conventional gamma camera.
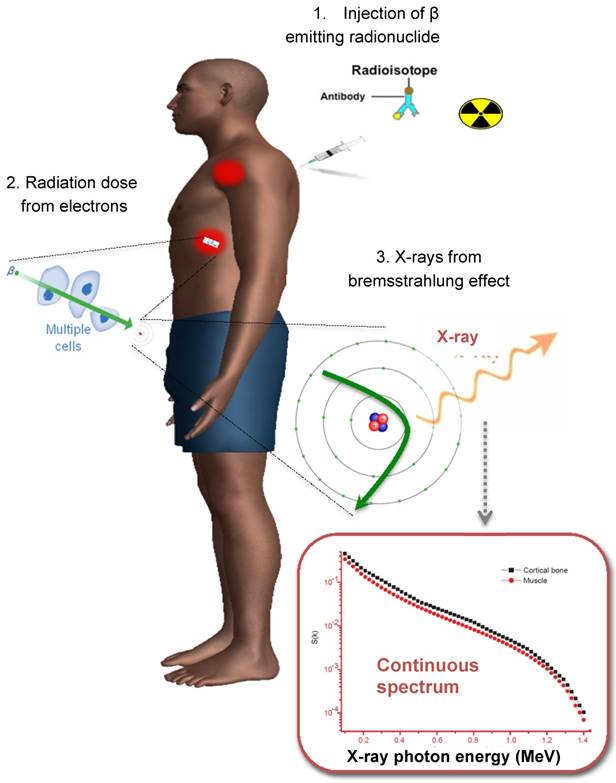
Quantification of bremsstrahlung images from beta emitters is very challenging due to its continuous energy spectrum. For example, high energy photons will be more likely to penetrate the collimator septa and detector crystal, whereas low energy photons have increased probability to be scattered. Rong et al. designed an optimal collimator for Y-90 bremsstrahlung SPECT imaging, with an 84 mm hole length, 3.5 mm hole diameter and 1.4 mm septal thickness [58]. Compared with the commercial high energy general purpose (HEGP) collimator, their design improved spatial resolution by 27%. Another challenge is that an effective attenuation coefficient is needed for AC due to the wide photon energy range [59]. Since there is no pronounced photopeak in the energy spectrum for bremsstrahlung radiation, selection of an optimal energy window is critical for quantification. Furthermore, traditional SC methods such as TEW are not suitable since the scattered photons cannot be distinguished from the primary photons in a continuous energy spectrum. Shen et al. studied the use of a Wiener filter to deconvolve septal penetration and scatter while suppressing image noise in planar Y-90 bremsstrahlung imaging, which used geometric mean of the conjugate view and effective point source methods for quantitation [60]. The estimated Y-90 activity for liver, spleen and 4 cm diameter tumors were within 17% and the cumulated activity was within 8% compared to the true value. In comparison, for 2 cm diameter tumors the activity and cumulated activity errors can increase to about 30% and 18%. Rong et al. proposed an OS-EM reconstruction algorithm incorporating multi-range SC and CDR modeling methods which can provide accurate estimates of organ activities [61]. They separated modeling of the primary bremsstrahlung and scattered photons with multiple energy ranges. ESSE scatter kernels, attenuation and CDR were also modeled and compensated for each subrange in the forward and back projection. This reduced the Y-90 activity quantitation error for all organs-of interest, especially the kidneys, by up to 27%. Roshan et al. reviewed the energy window selection, collimator design and reconstruction algorithm for Y-90 labeled microsphere bremsstrahlung imaging [62]. With a conventional medium energy general purpose collimator, a multiple-energy window with three energy peaks centered at 75 keV, 120 keV, and 185 keV with CT based AC and SC could achieve the highest system sensitivity and the lowest imaging acquisition time.
With the development of advanced techniques to improve image quality and quantitation, bremsstrahlung imaging is feasible to estimate organ activities in TRT. However, it is still limited by inferior spatial resolution, low number of counts, broad energy distribution, and severe scatter of bremsstrahlung photons. Pinhole or multi-pinhole collimators can improve the tradeoff between sensitivity and resolution in comparison with the conventional parallel-hole collimator for bremsstrahlung SPECT [63]. The better attenuating material used for pinhole collimation (tungsten rather than lead) could result in better bremsstrahlung SPECT performances. High-energy X-rays would down-scatter into the acquisition energy window, which would lead to a higher count-rate and substantial dead time effect, while scattering within the pinhole collimator is less of a problem for its empty cone geometry as compared to parallel-hole collimators [63]. However, the small field-of-view (FOV) of pinhole collimators is still a major problem for whole body TRT dosimetry.
Quantitative PET imaging
Compared to planar, SPECT and bremsstrahlung imaging, PET is more accurate in terms of in vivo activity quantification due to its superior spatial resolution, sensitivity and specificity for tumor detection. Image degradation factors in PET including random coincidences, detector normalization, dead time, attenuation and scatter need to be considered for TRT treatment planning [64]. The co-registered X-ray CT in PET/CT, or segmented MR images in PET/MR can be used for AC. Time-of-flight (TOF) imaging method is now a common specification in new PET scanners to provide a gain in image SNR [65], improved lesion detectability and more precise lesion uptake measurements. This merit can also be traded for reduced acquisition time or injection dose [66]. Additionally, immuno-PET was proposed as a quantitative imaging procedure to investigate the biological effect and pharmacokinetics of radioimmunotherapy agents, e.g., radiolabeled antibody in targeted and non-targeted tissues with high resolution [67, 68].
Similar to SPECT, the higher doses required for TRT can also be challenging for PET scanners with limited count-rate capability. The singles coming from secondary radiation or high-energy photons from non-pure annihilation effects lead to a higher random fraction. This is especially the case for Y-90 where the singles rate is relatively high and the positron branching ratio is very low, which leads to a higher random fraction. With a proper energy and coincidence window this effect can be reduced but it still contributes to the background signal.
Most PET theranostic isotopes are longer lived and emit high energy positrons with longer positron ranges as compared to F-18 whose mean positron range is 0.64 mm, limiting the best possible spatial resolution and quantification accuracy. For the latest generation of clinical PET systems, the reconstructed spatial resolution lies in the range of 4-6 mm and the positron range is relatively smaller. In preclinical imaging with a typical 1-2 mm reconstructed spatial resolution, this factor has a major impact. Several groups have investigated the impact of non-conventional isotopes on both spatial resolution and image contrast using high-resolution preclinical and clinical PET [69-71], and methods have been proposed for positron range correction. Derenzo et al. proposed a method to remove blurring in the filtered backprojected reconstructed images by Fourier deconvolution based on measured positron range functions [72]. Recently, methods incorporating isotope-specific positron range modelling into the maximum a posteriori (MAP) or OS-EM reconstruction algorithms have been developed [73-76]. Jødal L et al. provided the positron range distribution for some conventional and non-conventional isotopes by MCS. The results could be applied to image reconstruction algorithms to improve spatial resolution.
In order to fit the time activity curves for TRT agents with half-lives of typically 2-4 days [77], positron emitters with longer half-lives such as I-124 and Y-86 (100.2 h and 14.7 h) have been used in preclinical and clinical studies. Ideally, the positron emitters used for PET imaging are isotopes of the radionuclides in therapy, e.g. I-124 for I-131, and Y-86 for Y-90. However, I-124 and Y-86 are not pure positron emitters and they are associated with spurious coincidences such as prompt gamma coincidences (PGC), gamma-gamma cascades, intense bremsstrahlung radiation, and high-energy gamma rays that result in pair production [78]. Although most prompt gamma emissions have energy peaks higher than the upper bound of the PET energy window, they may still be down-scattered in the PET energy window and degrade image contrast [79]. For example, about 50% of the positrons are emitted with a 603-keV gamma photon simultaneously for I-124. Three gamma photons with energies of 1,077/1,854-keV, 628 and 443 keV are emitted simultaneously per Y-86 decay whose positron abundance is 32%. Background subtraction in the sinograms [80], empirical or analytical kernels for sinogram convolution [81] and recovery coefficient (RC) [82] have been proposed to resolve PGC. For Y-86 quantitation, Warland et al. proposed a patient-dependent method based on sinogram tail fitting with a Y-86 point spread function (PSF) library [81] to correct for PGC. The background and kidney activity errors in a phantom study were reduced from 117% to 9% and 84% to 5% respectively. In patient studies, the activity difference between total body scanning and urine sample was reduced from 92% to 7%. Buchholz et al. developed a scanner-dependent background subtraction method to correct for PGC [83]. They showed that quantification of Y-86 labeled radiotracers was feasible but they only evaluated simple cylindrical phantoms. Jentzen et al. estimated the RCs for I-124 in different PET/CT scanners [82]. Their results showed that after applying the RC, the error in activity estimation was ±10% for spheres ≥12.6 mm in diameter. However, RCs depend on different radionuclides and scanners which need to be determined respectively.
Lovqvist et al. compared the accuracy of biodistribution estimation between Y-86 PET and In-111 planar images in a nude mice model [84] when they acted as Y-90 imaging surrogates. The results showed that the uptake of In-111 and Y-86 was generally similar within the first 2 days post-injection but the activity of Y-86 was significantly higher than In-111 in most tissues at 4 days post-injection.
Instead of using Y-86 as surrogate, Y-90 also emits a few positrons via internal pair production and they are sufficient to be detected by PET. Gates et al. [85] and D'Arienzo M et al. [86] used conventional PET/CT scanners to detect the deposition of Y-90 microsphere directly. Comparing the performance of quantitative Y-90 bremsstrahlung and PET, Kao et al. concluded that Y-90 PET with advanced compensation techniques is superior in the aspects of image resolution, sensitivity and quantitation [87, 88], while Padia et al. showed that TOF Y-90 PET provided less scatter for comparable spatial resolution [89]. However, L(Y)SO, which is the most frequently used scintillator in PET nowadays, contains Lu-176, which is intrinsically radioactive and leads to a small background signal in the coincidence measurement. This effect is a potential limitation associated with Y-90 quantification due to the extremely low abundance of internal pair production for Y-90.
Motion blurring artifacts from patients' voluntary and involuntary motion, e.g., respiratory and cardiac motion, also affect image quantification. The use of respiratory gating with PET imaging has proven to be an efficient way to reduce motion blurring with minimal count loss or increase in scan time. Osborne et al. have shown that amplitude-based gating on Y-90 PET/CT images can be used to realize respiratory motion correction, which may further improve post-therapy dosimetry accuracy [90].
Table 3 summarizes the 4 radionuclide imaging techniques for TRT, highlighting their major features, limitations, and quantitative accuracy.
Overview of radionuclide imaging-based dosimetry for targeted radionuclide therapy.
| Imaging technique | Isotope | Energy window (keV) | Ref | Data source | Target region | Compensation technique and reconstruction algorithm | Key advantages of the method/ findings of the study | Limitations | Activity quantification errors |
|---|---|---|---|---|---|---|---|---|---|
| Planar | In-111 | 171±7%; 245±7% | [45] | Physical phantom and MCS | Critical organs and tumors | AC (projection of CT); SC (TEW: 152±4%, 205±10%); CDR; background and overlapping correction; | CPlanar method with full compensations | Organs overlap | Phantom: liver: -2.51%; heart: -3.21%; lungs: -17.22%; large sphere: -7.02%; small sphere: -28.95%; MCS: <48% for all organs |
| AC (projection of CT); SC (TEW: 152±4%, 205±10%); CDR; OS-EM. | QPlanar method partially solves organ overlap problem and allows more accurate modelling of image degradation factors | Required alignment between 3D organ VOIs and 2D planar projections; Assumed uniform activity distribution in each VOI | Phantom: liver: 3.22%; heart: 0.90%; lungs 7.61%; large sphere: -1.16%; small sphere: -0.59%; MCS: <14% for all organs | ||||||
| [46] | MCS and patient study | Critical organs | AC (CT); SC (TEW: 152±4%, 205±10%); CDR; OS-EM. | EQPlanar method combines whole body and individual organ rigid registration with background separation, partially improves the QPlanar method | Inferior quantification of small objects, e.g. tumors; Long computation time | MCS: <-7.12% for all organs; Patient: * | |||
| QSPECT | [47] | RSD torso phantom and MCS | Critical organs and tumors | AC (CT); SC (ESSE); CDR; PVC (pGTM) ; OS-EM. | Proposed a comprehensive SPECT quantitation method with model-based compensation methods | Assumed uniform uptake within each ROI when pGTM PVC modeling; Increased computation complexity | MCS: <5% for all organs except for lungs (11.47%); Phantom: <6.5%; except for the smaller sphere (-11.9%); | ||
| I-131 | 364±10% | [91] | MCS | Critical organs | AC (CT); SC (ESSE); CDR OS-EM. | Proposed model based down-scatter compensation for high energy photons | Increased computation comlexity | MCS: <2.5% for all organs, except for bone marrow (-9.33%) | |
| Lu-177 | 208±10% | [92] | Physical phantom and patient study | Tumors and critical organs | AC (CT); SC (APDI); OS-EM. | Investigated the feasibility and reliability of individualized dosimetry based on SPECT | No CDR and PVC was attempted; Increased computation complexity | Phantom: large tumors: (>16 ml) <20%; small tumors: (2.6 ml) <30%; Patient: * | |
| Ho-166 | 81±7.5% | [38] | Patient study | Tumors and critical organs | AC (CT); SC (TEW: 118±6% for down-scatter correction); OS-EM. | First validated the feasibility of quantitative MR imaging in TRT dosimetry by comparing with QSPECT result | MR should be imaged twice: before therapy (for anatomical info.); after Ho-166 admin. (for quantitation), which decreased the clinical feasibility | Patient: * | |
| Bremsstrahlung Imaging | Y-90 | 55-285 | [60] | Physical phantom | Critical organs and tumors | AC (linear effective coefficient or transmission scans); SC and septal penetration compensation | Use a Wiener filter to compensate for scatter and septal penetration | Simple geometry for physical phantom with homogeneous background and no overlapping sources | Phantom: individual activities <17% and cumulated activities <8% for all organs |
| 100-500 | [61] | Physical rod source phantom and MCS | Tumorsand critical organs | AC (CT); SC (ESSE); CDR; OS-EM. | Proposed a multi-range scatter and CDR modeling method | Increased computation complexity | MSC: <12 % for all organs; Phantom: large sphere: -7.0%; medium sphere: -9.7% and small sphere: -10.2% | ||
| PET | Y-86 | 350-650 | [81] | Physical phantom and patient study | Tumors and critical organs | AC (transmission scans); SC (sinograms convolution); dead time correction; OS-EM. | Proposed a patient dependent sinograms convolution based correction method for SC and PGC by providing tail fitting with PSF library | The count level reduced causing reduced SNR | Phantom: background: 9%; kidneys: 5%; Patient**: whole-body: <7% |
| I-124 | [93] | Physical thyroid phantom and rats | Tumors | AC (CT); dead time correction; FBP. | Used PET/CT for TRT dosimetry and validated it with phantom and small animal studies | Relative low positron emission of I-124 (~23%) degraded the image quality | Phantom: large sphere (250 ml): 2.86%; medium sphere (125 ml): 6.57%; small sphere (31 ml): -1.08%; Rats :* | ||
| Y-90 | [94] | Physical phantom and patient study | Tumors | Resolution recovery algorithm (TrueX); standard AC, SC, PVC and PGC correction; OS-EM. | TOF PET improved the contrast of hot-spheres | Slight deterioration in background variability | Phantom: total activity error 5%; large hot sphere: 8%; background: 1%; Patient :* |
Note: *For the clinical and preclinical study, no quantification errors were shown since the gold standard was unknown. **True activity=injected dose - activity in urine collections
Error source and uncertainty propagation for image-based 3D dosimetry
As described in Figure 1, uncertainties in image-based 3D dosimetry are attributed to many aspects including image degradation during the imaging process, dose calibration for system sensitivity measurement, volume-of-interest delineation, image registration, curve fitting, integration and dose conversion. It is important to acknowledge the potential sources and amplitude of errors for the final dose assessment on the critical organs and tumors. The quantitative errors from imaging have been described in detail in the previous sections. Other error sources are summarized as follows.
Dose calibration
To obtain quantitative bio-kinetic information of the radiopharmaceutical, it is essential to determine a calibration factor to convert the planar or reconstructed ECT voxel values into activity. The uncertainty caused by the determination of this calibration factor is dominant for QSPECT imaging based dosimetry [95].
Generally, there are two ways for measurement of the calibration factor (cps/MBq). The first is to acquire an image of a uniform phantom with known activity concentration [96]. The requisite calibration factor is equal to the known concentration in the phantom divided by the count in the ECT images. It can be used for other studies acquired using the same protocol and post-processing method. The second is to measure the calibration factor using a planar image of an in-air calibration source [97, 98]. In this method, the calibration factor is defined as the ratio between the background-corrected count rate in the whole image and the known source activity. The first approach using phantom calibration measurements is a more common approach. For SPECT imaging, if a parallel-hole collimator is used, then the measured calibration factor could be applied to all voxels within the FOV regardless of the source-to-collimator distance.
Volume-of-interest delineation
Determination of the VOIs is one of the most important steps in treatment planning and might affect the quantification accuracy by up to 30% [52]. The inferior spatial resolution and statistical noise on nuclear medicine images, as well as organs overlapping on the planar images impede the accuracy of image segmentation for VOI definition. Therefore, it is suggested that this step be performed on high resolution structural images such as CT and MRI, and then applied the VOIs to the registered ECT images after interpolations. Han et al. showed that the combination of functional and anatomical information can improve segmentation accuracy. They demonstrated that use of a graph cuts segmentation method based on both PET and CT data can yield 10% higher accuracy than using sole PET or CT data for tumors [99].
A well-designed segmentation method satisfies three conditions: accuracy, repeatability and efficiency, and according to different operational methods, segmentation for VOIs can be categorized as manual, semi-automatic and automatic methods. The accuracy of manual VOIs may easily be affected by blurred boundary due to the image resolution, PVE and operator's experience. Thus, automated or semi-automated techniques are often suggested for reducing inter-operator variation and time. Many state-of-the-art interactive segmentation algorithms for medical imaging applications have been proposed and are covered in several comprehensive reviews [100-102].
Image registration
In TRT, patients usually need to be imaged at different time points to obtain the time activity curve (TAC) and calculate organs' cumulative activity. However, patient movement and organ deformation are likely to happen between scans which may lead to reduced accuracy, especially for 3D dosimetry where cumulative activity needs to be generated on a voxel-by-voxel basis. Papavasileiou et al. showed that the differences in absorbed dose may be up to 90% even for small rigid mis-registration with translations <9.5 mm and rotations <6˚ [103]. These errors became more serious when the VOIs were distant from the center of the images. Therefore, registrations between serial nuclear medicine scans are essential for improved TRT dosimetry. Registration on quantitative functional images is challenging due to the lack of anatomic information, statistical noise after a large number of updates and isotope decay especially for later time points. Modern multi-modality scanners acquiring both ECT and high resolution anatomical images provide a feasible solution for this problem [104].
Moreover, non-rigid deformation in organ/tumor is more likely to happen in the clinical circumstance and rigid registration in most studies may not be adequate especially for small organs or lesions. Sjogreen et al. studied the impact of rigid or non-rigid registration of serial SPECT/CT images for TRT accuracy [105]. In their studies, rigid or non-rigid registration was performed on the CT images, and the deformation field obtained from the CT-CT registration was then employed to transform the corresponding SPECT images. They found that the activity estimation was more consistent after both rigid and non-rigid registrations. The differences between rigid and non-rigid registrations for residence time and absorbed dose in organs were small, but non-rigid registration had better precision especially in the anatomical regions where non-rigid movement was more likely to be present, e.g. neck and shoulder region. Ao et al. investigated the effect of using non-rigid local organ based registration on 3D dosimetric estimation, showing superior performance for non-rigid registration [106].
As multi-modality imaging techniques have shown merits for both segmentation and registration, sequential anatomical scans, e.g., low dose CT, might be considered to be included in the standard clinical TRT protocol in the near future.
Cumulative activity
Time integrated activity coefficients can be generated either by fitting an exponential function to each voxel and integrating the values of each voxel analytically over time or simply by a voxel-by-voxel numerical integration. One-phase, two-phase and multi-phase exponential decay models are used to describe the kinetic function of the targeted organs or tumors [43, 50, 107]. In the modeling process, 1 to 3 exponential terms can be selected. The sums of the exponentials are used as the model function of the TACs and are fitted for each organ.
Dose conversion
There are two main methodologies in TRT dosimetry: phantom-based and patient-specific dosimetry. For the MIRD phantom method [108, 109], a pre-calculated S factor is used to convert the activity to the mean absorbed dose that was calculated by MCS estimates for a referenced phantom. Due to the fixed organ size, shape and position, the MIRD method cannot achieve high dosimetric accuracy for patients with different anatomical variations, even though many adjustments have been proposed [110]. Moreover, only the mean absorbed dose at the organ-level can be obtained, which is not sufficient for pharmacokinetics evaluation.
To achieve dosimetry at the voxel level, one can use either dose-point kernel (DPK) convolution [111], MCS [112, 113] or voxel S values (VSVs) for dose conversion. In the late 90s, DPKs convolution with the 3D activity distribution was widely recommended for its efficiency compared with real-time MCS. The DPKs for electrons and photons, i.e., the mean absorbed dose per transition at a given radial distance for an isotropic point source located within an infinite homogeneous medium, can be pre-calculated for different isotopes [114, 115]. The VSVs approach was proposed to provide corresponding S values to the geometry of the voxel imaging data (e.g., SPECT, PET) and was adopted by the MIRD Committee [116, 117]. The local energy deposition (LED) method was proposed to simplify application of VSVs for pure beta emitters, and assumes that all kinetic energy released from beta emissions is locally absorbed within the source voxel. Thus, the 3D dose distribution can be calculated by simply multiplying the cumulated activity in a voxel with a unique dosimetric factor. Pasciak et al. showed that LED can reduce blurring effects on the activity concentration and is more accurate compared to VSVs using MCS method as the gold standard in a Y-90 microsphere SPECT study. This technique can further be applied to PET [118]. However, both DPK and VSV approaches cannot address the problem of tissue inhomogeneity. MCS-based dosimetry [119] is more accurate since it considers all the tissue variations within the patients, simulating particle transportation and energy deposition from all possible source organs. However, the intensive computation time impedes its clinical utility.
Uncertainty propagation for image-based dosimetry
Gustafsson J et al. investigated uncertainty propagation for image-based dosimetry by observing the decrease in standard deviation when removing a particular error source [120]. They used three anthropomorphic computer phantoms combined with a pharmacokinetic model of Lu-177-DOTATATE, modeling variations in calibration factor, noise on the CT-derived density map, dynamic activity distribution during SPECT data acquisition, VOI delineation and imaging starting time-points. The absorbed dose of the left kidney was investigated by excluding variations in factors mentioned above. They showed that the highest uncertainty in kidney absorbed dose appears to be the PVC using a fixed recovery coefficient and gamma camera calibration. The uncertainty propagation in quantitative PET based dosimetry (e.g., PGC, positron range correction) and PVC has not been systematically studied yet.
Except for the uncertainties attributed to image acquisition and post-processing, differences between the dose calibration and dosage administration time, residual activity remaining in the delivery system post administration, radionuclide impurities, and operator's errors also contribute to the overall errors in absorbed dose assessment, which can introduce errors in the prescribed dose after treatment planning or efficacy assessment after dose verification.
Conclusion
Quantitative imaging for TRT is challenging since most of the therapeutic agents are not optimal for imaging. The image generation methods for quantitative planar and ECT need to compensate many common image degradation factors for TRT agents, including down-scatter, bremsstrahlung photons and PGC, and researchers have obtained promising results for different isotopes. Conventional planar imaging quantification is still a common clinical choice for TRT due to its fast protocol for whole body imaging. However, accuracy is limited due to organ overlap and background activity. Although some advanced planar imaging techniques like QPlanar and EQPlanar can improve accuracy, the lack of 3D information impedes dosimetry at the voxel level. The limitations in planar imaging as well as the development of immuno-PET and TRT PET tracers prompt the use of SPECT/CT and PET/CT for more accurate quantification. PET possesses great potential for TRT due to its superior imaging characteristics and quantification, but availability of the technique and isotope is less widespread than SPECT/CT. For imaging gamma emitters such as I-131 and In-111, quantification errors within 10% can been obtained with different combinations of compensation [62]. For imaging positron emitters like Y-86 and I-124, quantitative errors are within 7% [81]. However, direct comparison of these methods is challenging as the studies were conducted using different phantoms, activity levels and imaging protocols.
Although the advantage of improved quantification for SPECT and PET as compared to planar imaging is apparent, optimization of imaging protocols with short acquisition times to cover the organs-of-interest or whole body imaging is important for routine clinical implementation. Moreover, advances in computing power, more advanced image reconstruction algorithms and compensation techniques, as well as associated hardware improvements (e.g., choices of collimator and detector) are essential to pursue high dosimetric accuracy. Yet the optimal way for quantitative imaging in TRT will probably be dependent on the distribution and object imaged, e.g., more scatter in a heavier patient.
The use of 3D quantitative ECT techniques is well recognized for TRT treatment planning and monitoring treatment response with high accuracy, while its merits await large scale clinical trials to demonstrate differences in therapeutic efficacy and clinical outcome for patients with and without receiving pre-treatment patient-specific dosimetry.
Abbreviations
TRT: targeted radionuclide therapy; ECT: emission computed tomography; Ho-166-PLLA-MS: Ho-166 labeled poly (L-lactic acid) microsphere; RE: radio-embolization; SIRT: selective internal radiation therapy; CPlanar: conventional planar; GM: geometric-mean; AC: attenuation correction; ROI: region-of-interest; QPlanar: quantitative planar; EQPlanar: extended QPlanar; VOI: volume-of-interest; QSPECT: quantitative SPECT; SC: scatter compensation; ESSE: effective source scatter estimation; PVC: partial volume compensation; pGTM: perturbation based geometric transfer matrix; CDR: collimator-detector-response; MCS: Monte Carlo simulation; RSD: radiology support device; APDI: interpolated analytical photon distribution; OS-EM: ordered subsets expectation maximization; PL-CT: penalized-likelihood function provided by the CT images; SNR: signal-to-noise ratio; TEW: triple energy window; HEGP: high energy general purpose; FOV: field-of-view; TOF: time-of-flight; MAP: maximum a posterior; PGC: prompt gamma coincidence; RC: recovery coefficient; PSF: point spread function; TAC: time activity curve; DPK: dose-point kernel; VSV: voxel S value; LED: local energy deposition.
Acknowledgements
The majority of this work was performed at the University of Macau. This work was supported by research grants from University of Macau (MYRG2016-00091-FST and MYRG2017-00060-FST), Fundo para o Desenvolvimento das Ciencias e da Tecnologia, Macau (114/2016/A3) and National Natural Science Foundation of China (81601525).
Competing Interests
The authors have declared that no competing interest exists.
References
1. Eary JF, Collins C, Stabin M, Vernon C, Petersdorf S, Baker M. et al. Samarium-153-EDTMP biodistribution and dosimetry estimation. J Nucl Med. 1993;34:1031-6
2. Waldherr C, Pless M, Maecke HR, Schumacher T, Crazzolara A, Nitzsche EU. et al. Tumor response and clinical benefit in neuroendocrine tumors after 7.4 GBq 90Y-DOTATOC. J Nucl Med. 2002;43:610-6
3. Vallabhajosula S, Kuji I, Hamacher KA, Konishi S, Kostakoglu L, Kothari PA. et al. Pharmacokinetics and biodistribution of 111In-and 177Lu-labeled J591 antibody specific for prostate-specific membrane antigen: prediction of 90Y-J591 radiation dosimetry based on 111In or 177Lu? J Nucl Med. 2005;46:634-41
4. Silberstein EB, Alavi A, Balon HR, Clarke SE, Divgi C, Gelfand MJ. et al. The SNMMI practice guideline for therapy of thyroid disease with 131I 3.0. J Nucl Med. 2012;53:1633-51
5. Sinha V, Goyel V, Trehan A. Radioactive microspheres in therapeutics. Pharmazie. 2004;59:419-26
6. National Research Council (US) Committee on the State of the Science of Nuclear Medicine. Advancing nuclear medicine through innovation. Washington, D.C. USA: National Academies Press. 2007
7. Prise KM. Bystander Effects and Radionuclide Therapy. In: (ed.) Stigbrand T, Carlsson J, Adams G. Targeted radionuclide tumor therapy. Dordrecht: Springer Publishing Company, LLC. 2008:311-9
8. Ersahin D, Doddamane I, Cheng D. Targeted radionuclide therapy. Cancers. 2011;3:3838-55
9. Pauwels S, Barone R, Walrand S, Borson-Chazot F, Valkema R, Kvols LK. et al. Practical dosimetry of peptide receptor radionuclide therapy with 90Y-labeled somatostatin analogs. J Nucl Med. 2005;46(Suppl 1):92S-8S
10. Luster M, Clarke S, Dietlein M, Lassmann M, Lind P, Oyen W. et al. Guidelines for radioiodine therapy of differentiated thyroid cancer. Eur J Nucl Med Mol Imaging. 2008;35:1941-59
11. Kulkarni K, Nostrand DV, Atkins F, Aiken M, Burman K, Wartofsky L. The relative frequency in which empiric dosages of radioiodine would potentially overtreat or undertreat patients who have metastatic well-differentiated thyroid cancer. Thyroid. 2006;16:1019-23
12. de Keizer B, Brans B, Hoekstra A, Zelissen PM, Koppeschaar HP, Lips CJ. et al. Tumour dosimetry and response in patients with metastatic differentiated thyroid cancer using recombinant human thyrotropin before radioiodine therapy. Eur J Nucl Med Mol Imaging. 2003;30:367-73
13. Strigari L, Konijnenberg M, Chiesa C, Bardies M, Du Y, Gleisner KS. et al. The evidence base for the use of internal dosimetry in the clinical practice of molecular radiotherapy. Eur J Nucl Med Mol Imaging. 2014;41:1976-88
14. Stabin MG. Uncertainties in internal dose calculations for radiopharmaceuticals. J Nucl Med. 2008;49:853-60
15. Erdi AK, Erdi YE, Yorke ED, Wessels BW. Treatment planning for radio-immunotherapy. Phys Med Biol. 1996;41:2009
16. Bardiès M, Flux G, Lassmann M, Monsieurs M, Savolainen S, Strand S-E. Quantitative imaging for clinical dosimetry. Nucl Instrum Methods Phys Res A. 2006;569:467-71
17. Ljungberg M, Gleisner KS. Hybrid Imaging for patient-specific dosimetry in radionuclide therapy. Diagnostics. 2015;5:296-317
18. Ljungberg M, Sjögreen Gleisner K. Personalized Dosimetry for Radionuclide Therapy Using Molecular Imaging Tools. Biomedicines. 2016;4:25
19. Funkhouser J. Reinventing pharma: The theranostic revolution. Curr Drug Discov. 2002;2:17-9
20. Smits ML, Nijsen JF, van den Bosch MA, Lam MG, Vente MA, Huijbregts JE. et al. Holmium-166 radioembolization for the treatment of patients with liver metastases: design of the phase I HEPAR trial. J Exp Clin Cancer Res. 2010;29:1
21. Smits ML, Nijsen JF, van den Bosch MA, Lam MG, Vente MA, Mali WP. et al. Holmium-166 radioembolisation in patients with unresectable, chemorefractory liver metastases (HEPAR trial): a phase 1, dose-escalation study. Lancet Oncol. 2012;13:1025-34
22. Vente MA, Nijsen JF, de Roos R, van Steenbergen MJ, Kaaijk C, Koster-Ammerlaan MJ. et al. Neutron activation of holmium poly (L-lactic acid) microspheres for hepatic arterial radioembolization: a validation study. Biomed Microdevices. 2009;11:763-72
23. Loke KS, Padhy AK, Ng DC, Goh AS, Divgi C. Dosimetric considerations in radioimmunotherapy and systemic radionuclide therapies: a review. World J Nucl Med. 2011;10:122
24. Plyku D, Hobbs RF, Huang K, Atkins F, Garcia C, Sgouros G. et al. Recombinant human thyroid-stimulating hormone versus thyroid hormone withdrawal in 124I-PET/CT based dosimetry for 131I therapy of metastatic differentiated thyroid cancer. J Nucl Med. 2017;58:1146-54
25. Boucek JA, Turner JH. Personalized dosimetry of 131I-rituximab radioimmunotherapy of non-Hodgkin lymphoma defined by pharmacokinetics in bone marrow and blood. Cancer Biother Radiopharm. 2014;29:18-25
26. Bombardieri E, Giammarile F, Aktolun C, Baum RP, Delaloye AB, Maffioli L. et al. 131I/123I-metaiodobenzylguanidine (mIBG) scintigraphy: procedure guidelines for tumour imaging. Eur J Nucl Med Mol Imaging. 2010;37:2436-46
27. Dieudonné A, Garin E, Laffont S, Rolland Y, Lebtahi R, Leguludec D. et al. Clinical feasibility of fast 3-dimensional dosimetry of the liver for treatment planning of hepatocellular carcinoma with 90Y-microspheres. J Nucl Med. 2011;52:1930-7
28. Rizvi SN, Visser OJ, Vosjan MJ, van Lingen A, Hoekstra OS, Zijlstra JM. et al. Biodistribution, radiation dosimetry and scouting of 90Y-ibritumomab tiuxetan therapy in patients with relapsed B-cell non-Hodgkin's lymphoma using 89Zr-ibritumomab tiuxetan and PET. Eur J Nucl Med Mol Imaging. 2012;39:512-20
29. Wiseman GA, Leigh B, Erwin WD, Lamonica D, Kornmehl E, Spies SM. et al. Radiation dosimetry results for zevalin radioimmunotherapy of rituximab-refractory non-hodgkin lymphoma. Cancer. 2002;94:1349-57
30. Förster GJ, Engelbach M, Brockmann J, Reber H, Buchholz H-G, Mäcke HR. et al. Preliminary data on biodistribution and dosimetry for therapy planning of somatostatin receptor positive tumours: comparison of 86Y-DOTATOC and 111In-DTPA-octreotide. Eur J Nucl Med. 2001;28:1743-50
31. Helisch A, Förster GJ, Reber H, Buchholz H-G, Arnold R, Göke B. et al. Pre-therapeutic dosimetry and biodistribution of 86Y-DOTA-Phe1-Tyr3-octreotide versus 111In-pentetreotide in patients with advanced neuroendocrine tumours. Eur J Nucl Med Mol Imaging. 2004;31:1386-92
32. Cremonesi M, Ferrari M, Zoboli S, Chinol M, Stabin MG, Orsi F. et al. Biokinetics and dosimetry in patients administered with 111 In-DOTA-Tyr 3-octreotide: implications for internal radiotherapy with 90 Y-DOTATOC. Eur J Nucl Med Mol Imaging. 1999;26:877-86
33. Forrer F, Uusijärvi H, Waldherr C, Cremonesi M, Bernhardt P, Mueller-Brand J. et al. A comparison of 111In-DOTATOC and 111In-DOTATATE: biodistribution and dosimetry in the same patients with metastatic neuroendocrine tumours. Eur J Nucl Med Mol Imaging. 2004;31:1257-62
34. Kwekkeboom DJ, Bakker WH, Kooij PP, Konijnenberg MW, Srinivasan A, Erion JL. et al. [177 Lu-DOTA 0, Tyr 3] octreotate: comparison with [111 In-DTPA 0] octreotide in patients. Eur J Nucl Med Mol Imaging. 2001;28:1319-25
35. Stabin M, Kooij P, Bakker W, Inoue T. Radiation dosimetry for indium-111-pentetreotide. J Nucl Med. 1997;38:1919
36. Baum RP, Kulkarni HR, Schuchardt C, Singh A, Wirtz M, Wiessalla S. et al. Lutetium-177 PSMA radioligand therapy of metastatic castration-resistant prostate cancer: safety and efficacy. J Nucl Med. 2016;57:1006-13
37. Breitz H, Wendt R, Stabin M, Bouchet L, Wessels B. Dosimetry of high dose skeletal targeted radiotherapy (STR) with 166Ho-DOTMP. Cancer Biother Radiopharm. 2003;18:225-30
38. Smits ML, Elschot M, van den Bosch MA, van de Maat GH, van het Schip AD, Zonnenberg BA. et al. In vivo dosimetry based on SPECT and MR imaging of 166Ho-microspheres for treatment of liver malignancies. J Nucl Med. 2013;54:2093-100
39. Vigna L, Matheoud R, Ridone S, Arginelli D, Della Monica P, Rudoni M. et al. Characterization of the [153 Sm] Sm-EDTMP pharmacokinetics and Estimation of radiation absorbed dose on an individual Basis. Phys Med. 2011;27:144-52
40. Blake GM, Zivanovic MA, Blaquiere RM, Fine DR, McEwan AJ, Ackery DM. Strontium-89 therapy: measurement of absorbed dose to skeletal metastases. J Nucl Med. 1988;29:549-57
41. Liepe K, Hliscs R, Kropp J, Runge R, Knapp FFR, Franke W-G. Dosimetry of 188Re-hydroxyethylidene diphosphonate in human prostate cancer skeletal metastases. J Nucl Med. 2003;44:953-60
42. Thomas SR, Maxon HR, Kereiakes JG. Invivo quantitation of lesion radioactivity using external counting methods. Med Phys. 1976;3:253-5
43. He B, Wahl RL, Du Y, Sgouros G, Jacene H, Flinn I. et al. Comparison of residence time estimation methods for radioimmunotherapy dosimetry and treatment planning—Monte Carlo simulation studies. IEEE Trans Med Imaging. 2008;27:521-30
44. Sjögreen K, Ljungberg M, Strand S-E. An activity quantification method based on registration of CT and whole-body scintillation camera images, with application to 131I. J Nucl Med. 2002;43:972-82
45. He B, Frey EC. Comparison of conventional, model-based quantitative planar, and quantitative SPECT image processing methods for organ activity estimation using In-111 agents. Phys Med Biol. 2006;51:3967
46. Song N, He B, Wahl R, Frey E. EQPlanar: a maximum-likelihood method for accurate organ activity estimation from whole body planar projections. Phys Med Biol. 2011;56:5503
47. He B, Du Y, Song X, Segars WP, Frey EC. A Monte Carlo and physical phantom evaluation of quantitative In-111 SPECT. Phys Med Biol. 2005;50:4169
48. Frey EC, Tsui B. A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. IEEE Nucl Sci Symp Conf Rec (1997). 1996;2:1082-6
49. Du Y, Tsui BM, Frey EC. Partial volume effect compensation for quantitative brain SPECT imaging. IEEE Trans Med Imaging. 2005;24:969-76
50. He B, Frey EC. Effects of shortened acquisition time on accuracy and precision of quantitative estimates of organ activity. Med Phys. 2010;37:1807
51. Vandervoort E, Celler A, Wells G, Blinder S, Dixon K, Pang Y. Implementation of an analytically based scatter correction in SPECT reconstructions. IEEE Trans Nucl Sci. 2005;52:645-53
52. Shcherbinin S, Celler A, Belhocine T, Vanderwerf R, Driedger A. Accuracy of quantitative reconstructions in SPECT/CT imaging. Phys Med Biol. 2008;53:4595-604
53. Tsui BMW, Frey EC, Xide Z, Lalush DS, Johnston RE, McCartney WH. The importance and implementation of accurate 3D compensation methods for quantitative SPECT. Phys Med Biol. 1994;39:509
54. Dewaraja YK, Koral KF, Fessler JA. Regularized reconstruction in quantitative SPECT using CT side information from hybrid imaging. Phys Med Biol. 2010;55:2523-39
55. Seo Y, Wong KH, Hasegawa BH. Calculation and validation of the use of effective attenuation coefficient for attenuation correction in In-111 SPECT. Med Phys. 2005;32:3628-35
56. Ljungberg M, Celler A, Konijnenberg MW, Eckerman KF, Dewaraja YK, Sjögreen-Gleisner K. MIRD Pamphlet No. 26: Joint EANM/MIRD Guidelines for Quantitative 177Lu SPECT applied for Dosimetry of Radiopharmaceutical Therapy. J Nucl Med. 2016;57:151-62
57. He B, Nikolopoulou A, Osborne J, Vallabhajosula S, Goldsmith S. Quantitative SPECT imaging with Lu-177: A physical phantom evaluation. J Nucl Med. 2012;53(Suppl 1):2407
58. Rong X, Frey EC. A collimator optimization method for quantitative imaging: Application to Y-90 bremsstrahlung SPECT. Med Phys. 2013;40:082504
59. Clarke LP, Cullom SJ, Shaw R, Reece C, Penney BC, King MA. et al. Bremsstrahlung imaging using the gamma camera: factors affecting attenuation. J Nucl Med. 1992;33:161-6
60. Shen S, DeNardo GL, DeNardo SJ. Quantitative bremsstrahlung imaging of yttrium-90 using a Wiener filter. Med Phys. 1994;21:1409-17
61. Rong X, Du Y, Ljungberg M, Rault E, Vandenberghe S, Frey EC. Development and evaluation of an improved quantitative 90Y bremsstrahlung SPECT method. Med Phys. 2012;39:2346-58
62. Roshan H, Azarm A, Mahmoudian B, Islamian J. Advances in SPECT for Optimizing the Liver Tumors Radioembolization Using Yttrium-90 Microspheres. World J Nucl Med. 2015;14:75
63. Walrand S, Hesse M, Demonceau G, Pauwels S, Jamar F. Yttrium-90-labeled microsphere tracking during liver selective internal radiotherapy by bremsstrahlung pinhole SPECT: feasibility study and evaluation in an abdominal phantom. EJNMMI Res. 2011;1:1
64. Zanzonico P. Positron emission tomography: a review of basic principles, scanner design and performance, and current systems. Semin Nucl Med. 2004;34:87-111
65. SNM: Karp JS, Fletcher JW. Time-of-flight PET. PET Center of Excellence Newsletter. 2006. http://www.iss.infn.it/topem/TOF-PET/timeofflightpet.pdf
66. Surti S. Update on time-of-flight PET imaging. J Nucl Med. 2015;56:98-105
67. Boerman OC, Oyen WJ. Immuno-PET of cancer: a revival of antibody imaging. J Nucl Med. 2011;52:1171-2
68. Van Dongen GA, Visser GW, Lub-de Hooge MN, De Vries EG, Perk LR. Immuno-PET: a navigator in monoclonal antibody development and applications. Oncologist. 2007;12:1379-89
69. Laforest R, Rowland DJ, Welch MJ. MicroPET imaging with nonconventional isotopes. IEEE Trans Nucl Sci. 2002;49:2119-26
70. Liu X, Laforest R. Quantitative small animal PET imaging with nonconventional nuclides. Nucl Med Biol. 2009;36:551-9
71. Disselhorst JA, Brom M, Laverman P, Slump CH, Boerman OC, Oyen WJ. et al. Image-quality assessment for several positron emitters using the NEMA NU 4-2008 standards in the Siemens Inveon small-animal PET scanner. J Nucl Med. 2010;51:610-7
72. Derenzo SE. Mathematical removal of positron range blurring in high resolution tomography. IEEE Trans Nucl Sci. 1986;33:565-9
73. Bai B, Ruangma A, Laforest R, Tai Y-C, Leahy RM. Positron range modeling for statistical PET image reconstruction. IEEE Nucl Sci Symp Conf Rec (1997). 2003:2501-5
74. Bai B, Laforest R, Smith AM, Leahy RM. Evaluation of MAP image reconstruction with positron range modeling for 3D PET. IEEE Nucl Sci Symp Conf Rec (1997). 2005:2686-9
75. Fu L, Qi J. A novel iterative image reconstruction method for high-resolution PET Imaging with a Monte Carlo based positron range model. IEEE Nucl Sci Symp Conf Rec (1997). 2008:3609-12
76. Cal-González J, Herraiz J, España S, Desco M, Vaquero JJ, Udías JM. Positron range effects in high resolution 3D PET imaging. IEEE Nucl Sci Symp Conf Rec (1997). 2009:2788-91
77. Verel I, Visser GW, van Dongen GA. The promise of immuno-PET in radioimmunotherapy. J Nucl Med. 2005;46(Suppl 1):164S-71S
78. Conti M, Eriksson L. Physics of pure and non-pure positron emitters for PET: a review and a discussion. EJNMMI Phys. 2016;3:1-17
79. Lubberink M, Herzog H. Quantitative imaging of 124I and 86Y with PET. Eur J Nucl Med Mol Imaging. 2011;38:10-8
80. Lubberink M, Schneider H, Bergström M, Lundqvist H. Quantitative imaging and correction for cascade gamma radiation of 76Br with 2D and 3D PET. Phys Med Biol. 2002;47:3519
81. Walrand S, Jamar F, Mathieu I, De Camps J, Lonneux M, Sibomana M. et al. Quantitation in PET using isotopes emitting prompt single gammas: application to yttrium-86. Eur J Nucl Med Mol Imaging. 2003;30:354-61
82. Jentzen W, Weise R, Kupferschläger J, Freudenberg L, Brandau W, Bares R. et al. Iodine-124 PET dosimetry in differentiated thyroid cancer: recovery coefficient in 2D and 3D modes for PET (/CT) systems. Eur J Nucl Med Mol Imaging. 2008;35:611-23
83. Buchholz HG, Herzog H, Förster GJ, Reber H, Nickel O, Rösch F. et al. PET imaging with yttrium-86: comparison of phantom measurements acquired with different PET scanners before and after applying background subtraction. Eur J Nucl Med Mol Imaging. 2003;30:716-20
84. Lövqvist A, Humm JL, Sheikh A, Finn RD, Koziorowski J, Ruan S. et al. PET imaging of 86Y-labeled anti-Lewis Y monoclonal antibodies in a nude mouse model: comparison between 86Y and 111In radiolabels. J Nucl Med. 2001;42:1281-7
85. Gates VL, Esmail AA, Marshall K, Spies S, Salem R. Internal pair production of 90Y permits hepatic localization of microspheres using routine PET: proof of concept. J Nucl Med. 2011;52:72-6
86. D'Arienzo M, Chiaramida P, Chiacchiararelli L, Coniglio A, Cianni R, Salvatori R. et al. 90Y PET-based dosimetry after selective internal radiotherapy treatments. Nucl Med Commun. 2012;33:633-40
87. Kao Y-H, Steinberg JD, Tay Y-S, Lim GK, Yan J, Townsend DW. et al. Post-radioembolization yttrium-90 PET/CT-part 1: diagnostic reporting. EJNMMI Res. 2013;3:56
88. Kao Y-H, Steinberg JD, Tay Y-S, Lim GK, Yan J, Townsend DW. et al. Post-radioembolization yttrium-90 PET/CT-part 2: dose-response and tumor predictive dosimetry for resin microspheres. EJNMMI Res. 2013;3:57
89. Padia SA, Alessio A, Kwan SW, Lewis DH, Vaidya S, Minoshima S. Comparison of positron emission tomography and bremsstrahlung imaging to detect particle distribution in patients undergoing yttrium-90 radioembolization for large hepatocellular carcinomas or associated portal vein thrombosis. J Vasc Interv Radiol. 2013;24:1147-53
90. Osborne DR, Acuff S, Neveu M, Kaman A, Syed M, Fu Y. 90Y Liver Radioembolization Imaging Using Amplitude-Based Gated PET/CT. Clin Nucl Med. 2017;42:373-4
91. Song N, Du Y, He B, Frey EC. Development and evaluation of a model-based downscatter compensation method for quantitative I-131 SPECT. Med Phys. 2011;38:3193
92. Hippeläinen E, Tenhunen M, Mäenpää H, Sohlberg A. Quantitative accuracy of 177 Lu SPECT reconstruction using different compensation methods: phantom and patient studies. EJNMMI Res. 2016;6:1
93. El-Ali HH, Eckerwall M, Skovgaard D, Larsson E, Strand S-E, Kjaer A. The Combination of In vivo 124I-PET and CT small animal imaging for evaluation of thyroid physiology and dosimetry. Diagnostics (Basel). 2012;2:10-22
94. Willowson K, Forwood N, Jakoby BW, Smith AM, Bailey DL. Quantitative 90Y image reconstruction in PET. Med Phys. 2012;39:7153-9
95. Zeintl J, Vija AH, Yahil A, Hornegger J, Kuwert T. Quantitative accuracy of clinical 99mTc SPECT/CT using ordered-subset expectation maximization with 3-dimensional resolution recovery, attenuation, and scatter correction. J Nucl Med. 2010;51:921-8
96. Koral KF, Zasadny KR, Kessler ML, Luo J-Q, Buchbinder SF, Kaminski MS. et al. CT-SPECT fusion plus conjugate views for determining dosimetry in iodine-131-monoclonal antibody therapy of lymphoma patients. J Nucl Med. 1994;35:1714-20
97. Ljungberg M, Frey E, Sjögreen K, Liu X, Dewaraja Y, Strand S-E. 3D absorbed dose calculations based on SPECT: evaluation for 111-In/90-Y therapy using Monte Carlo simulations. Cancer Biother Radiopharm. 2003;18:99-107
98. Anizan N, Wang H, Zhou XC, Hobbs RF, Wahl RL, Frey EC. Factors affecting the stability and repeatability of gamma camera calibration for quantitative imaging applications based on a retrospective review of clinical data. EJNMMI Res. 2014;4:67
99. Han D, Bayouth J, Song Q, Taurani A, Sonka M, Buatti J. et al. Globally optimal tumor segmentation in PET-CT images: A graph-based co-segmentation method. Inf Process Med Imaging. 2011;22:245-56
100. Schenk A, Prause G, Peitgen H-O. Efficient semiautomatic segmentation of 3D objects in medical images. Med Image Comput Comput Assist Interv. 2000;1935:186-95
101. Zhang H, Fritts JE, Goldman SA. Image segmentation evaluation: A survey of unsupervised methods. Comput Vis Image Underst. 2008;110:260-80
102. McGuinness K, O'connor NE. A comparative evaluation of interactive segmentation algorithms. Pattern Recognit. 2010;43:434-44
103. Papavasileiou P, Divoli A, Hatziioannou K, Flux GD. The importance of the accuracy of image registration of SPECT images for 3D targeted radionuclide therapy dosimetry. Phys Med Biol. 2007;52:N539-N48
104. Townsend DW, Carney JP, Yap JT, Hall NC. PET/CT today and tomorrow. J Nucl Med. 2004;45:4S-14S
105. Sjögreen-Gleisner K, Rueckert D, Ljungberg M. Registration of serial SPECT/CT images for three-dimensional dosimetry in radionuclide therapy. Phys Med Biol. 2009;54:6181-200
106. Ao EC, Wu NY, Wang SJ, Song N, Mok GS. Improved dosimetry for targeted radionuclide therapy using nonrigid registration on sequential SPECT images. Med Phys. 2015;42:1060-70
107. He B, Du Y, Segars WP, Wahl RL, Sgouros G, Jacene H. et al. Evaluation of quantitative imaging methods for organ activity and residence time estimation using a population of phantoms having realistic variations in anatomy and uptake. Med Phys. 2009;36:612-9
108. Loevinger R, Berman M. Schema for absorbed-dose calculations for biologically-distributed radionuclides. J Nucl Med. 1968;9(Suppl 1):9-14
109. Loevinger R, Berman M. A revised schema for calculating the absorbed dose from biologically distributed radionuclides. MIRD Pamphlet No. 1. Revised ed. New York, NY: Society of Nuclear Medicine. 1976
110. Stabin MG, Brill AB. State of the Art in Nuclear Medicine Dose Assessment. Semin Nucl Med. 2008;38:308-20
111. Loevinger R, Japha E, Brownell G. Discrete radioisotope sources. In: (ed.) Hine GJ, Brownell GL. Radiation dosimetry. New York, NY: Academic Press. 1956:693-799
112. Furhang EE, Chui CS, Sgouros G. A Monte Carlo approach to patient-specific dosimetry. Med Phys. 1996;23:1523-9
113. Furhang EE. Chui CS, Kolbert KS, Larson SM, Sgouros G. Implementation of a Monte Carlo-based dosimetry method for patient-specific internal emitter therapy. Med Phys. 1997;24:1163-72
114. Tagesson M, Ljungberg M, Strand S-E. A Monte Carlo program converting activity distributions to absorbed dose distributions in a radionuclide treatment planning system. Acta Oncol. 1996;35:367-72
115. Ferrer L, Chouin N, Bitar A, Lisbona A, Bardiès M. Implementing dosimetry in GATE: Dose-point kernel validation with GEANT4 4.8. 1. Cancer Biother Radiopharm. 2007;22:125-9
116. Liu A, Williams LE, Wong JY, Raubitschek AA. Monte Carlo-assisted voxel source kernel method (MAVSK) for internal beta dosimetry. Nucl Med Biol. 1998;25:423-33
117. Bolch WE, Bouchet LG, Robertson JS, Wessels BW. MIRD pamphlet No, 17: The dosimetry of nonuniform activity distributions-radionuclide S values at the voxel level. J Nucl Med. 1999;40:S11
118. Pasciak AS, Erwin WD. Effect of voxel size and computation method on Tc-99m MAA SPECT/CT-based dose estimation for Y-90 microsphere therapy. IEEE Trans Med Imaging. 2009;28:1754-8
119. Furhang EE, Chui CS, Kolbert KS, Larson SM, Sgouros G. Implementation of a Monte Carlo dosimetry method for patient-specific internal emitter therapy. Med Phys. 1997;24:1163
120. Gustafsson J, Brolin G, Cox M, Ljungberg M, Johansson L, Gleisner KS. Uncertainty propagation for SPECT/CT-based renal dosimetry in 177Lu peptide receptor radionuclide therapy. Phys Med Biol. 2015;60:8329
Author contact
![]() Corresponding authors: Stefaan Vandenberghe: Electronic mail: Stefaan.Vandenberghebe; Telephone: (32) 093325854. Greta S. P. Mok: Electronic mail: gretamokmo; Telephone: (853) 8822-4491.
Corresponding authors: Stefaan Vandenberghe: Electronic mail: Stefaan.Vandenberghebe; Telephone: (32) 093325854. Greta S. P. Mok: Electronic mail: gretamokmo; Telephone: (853) 8822-4491.
 Global reach, higher impact
Global reach, higher impact