PDF

Theranostics 2019; 9(11):3365-3387. doi:10.7150/thno.34509 This issue Cite

Review

Research tools for extrapolating the disposition and pharmacokinetics of nanomaterials from preclinical animals to humans

Michael S. Valic¹, Gang Zheng^1,2

1. Princess Margaret Cancer Centre, University Health Network, Toronto, Ontario, CANADA, M5G 1L7.
2. Department of Medical Biophysics, Institute of Biomaterials and Biomedical Engineering, and Leslie Dan Faculty of Pharmacy, University of Toronto, Toronto, Ontario, CANADA, M5G 1L7.

✉ Corresponding author: Prof. Gang Zheng, 101 College Street, PMCRT 5-354, Toronto, Ontario, CANADA, M5G 1L7. 416-581-7666 (Office) gang.zhengca

Abstract

A critical step in the translational science of nanomaterials from preclinical animal studies to humans is the comprehensive investigation of their disposition (or ADME) and pharmacokinetic behaviours. Disposition and pharmacokinetic data are ideally collected in different animal species (rodent and nonrodent), at different dose levels, and following multiple administrations. These data are used to assess the systemic exposure and effect to nanomaterials, primary determinants of their potential toxicity and therapeutic efficacy. At toxic doses in animal models, pharmacokinetic (termed toxicokinetic) data are related to toxicologic findings that inform the design of nonclinical toxicity studies and contribute to the determination of the maximum recommended starting dose in clinical phase 1 trials. Nanomaterials present a unique challenge for disposition and pharmacokinetic investigations owing to their prolonged circulation times, nonlinear pharmacokinetic profiles, and their extensive distribution into tissues. Predictive relationships between nanomaterial physicochemical properties and behaviours in vivo are lacking and are confounded by anatomical, physiological, and immunological differences amongst preclinical animal models and humans. These challenges are poorly understood and frequently overlooked by investigators, leading to inaccurate assumptions of disposition, pharmacokinetic, and toxicokinetics profiles across species that can have profoundly detrimental impacts for nonclinical toxicity studies and clinical phase 1 trials. Herein are highlighted two research tools for analysing and interpreting disposition and pharmacokinetic data from multiple species and for extrapolating this data accurately in humans. Empirical methodologies and mechanistic mathematical modelling approaches are discussed with emphasis placed on important considerations and caveats for representing nanomaterials, such as the importance of integrating physiological variables associated with the mononuclear phagocyte system (MPS) into extrapolation methods for nanomaterials. The application of these tools will be examined in recent examples of investigational and clinically approved nanomaterials. Finally, strategies for applying these extrapolation tools in a complementary manner to perform dose predictions and in silico toxicity assessments in humans will be explained. A greater familiarity with the available tools and prior experiences of extrapolating nanomaterial disposition and pharmacokinetics from preclinical animal models to humans will hopefully result in a more straightforward roadmap for the clinical translation of promising nanomaterials.

Keywords: nanomaterials, ADME, pharmacokinetics, interspecies allometric scaling, physiologically based pharmacokinetic modelling

Introduction

Nano-scale biomaterials (nanomaterials) developed for applications in medical imaging and therapy span a diverse range of chemistries, compositions, and physical and biological properties. A critical step in the development of these nanomaterial platforms is elucidating measurable relationships between physicochemical properties and in vivo disposition (absorption, distribution, metabolism, and excretion, known by the acronym ADME) and pharmacokinetics—the mathematical description of the rates of ADME processes and of concentration-time relationships. A major breakthrough in this regard was the discovery that coating liposomes with polyethylene glycol (PEG), a synthetic hydrophilic polymer, significantly prolonged their circulation times in vivo by as much as 5-fold [1, 2]. Overcoming the rapid clearance kinetics of the mononuclear phagocyte system (MPS) was important for realising more useful functions of many nanomaterial types, such as for delivering imaging agents or drugs to sites of disease via the enhanced permeability and retention (EPR) effect. Since then numerous strategies have been developed to improve nanomaterial pharmacokinetics, from camouflaging nanomaterials for reduced interaction with plasma opsins [3-5] to sophisticated approaches for delaying or circumventing MPS clearance [6, 7].

Studying nanomaterial disposition and pharmacokinetics is a far more challenging and nuanced endeavour than given credit. Investigators often overlook important anatomical, physiological, biochemical, and immunological differences between species used to perform these studies (typically rats and beagle dogs) and humans [8, 9], differences that may be consequential for understanding and interpreting nanomaterial behaviours in vivo. These differences may also violate key size-dependency assumptions underlying extrapolation methods that, if unrecognised, will lead to scaling relationships or mechanistic models that cannot accurately extrapolate disposition and pharmacokinetics in humans. The consequences of failing to account for these differences when investigating and extrapolating nanomaterial pharmacokinetics and toxicokinetics have been previously reported: from the selection of unsuitable animal models for performing pharmacokinetic and toxicokinetic studies [10], to significant underestimations of maximum recommended starting dose (MRSD) for conducting human phase 1 clinical trials [11]. Having knowledge of these challenges and the strategies for addressing them prior to commencing comprehensive multispecies investigations of pharmacokinetics and toxicity can greatly limit the risks and uncertainties in the clinical development of promising candidate nanomaterials.

The key to overcoming many of these challenges is to establish a roadmap combining the best practices and prior experiences of extrapolating investigational nanomaterial pharmacokinetics from animal models to humans. Towards this end, highlighted here are research tools for analysing and interpreting disposition and pharmacokinetic data of parenteral (intravenous) nanomaterials in multiple species (Figure 1). Allometric principles for extrapolating nanomaterial pharmacokinetic data accurately in humans are discussed with recent examples of investigational and clinically approved nanomaterials. State-of-the-art modelling methodologies for creating mechanistic representations of nanomaterial disposition and pharmacokinetics are also explored with practical examples for simulating disposition and pharmacokinetic, and for assessing toxicity in silico. Throughout will be particular emphasis for the considerations and caveats of applying these tools with the diverse physicochemical properties and in vivo behaviours nanomaterials manifest. Finally, the best practices for leveraging extrapolation tools to perform dose selection of investigational nanomaterials for clinical phase 1 trials and in silico toxicity assessments in humans will be explained.

Extrapolating nanomaterial pharmacokinetics from preclinical animal models to humans using allometric scaling and correlative analyses

An introduction to allometry and interspecies allometric scaling

In the context of biological scaling, allometry describes any anatomical or physiological property whose proportional relationship with the mass or geometry (surface area and volume) of an organism deviates from the constant proportions predicted by isometry. Many physiological and biochemical processes (e.g., basal metabolic rate (BMR), blood circulation time, glomerular filtration rate (GFR), etc.) and anatomical structures (e.g., heart, kidney, and liver weights, surface area, etc.) exhibit allometric relationships with the body weight or body-surface area in various mammalian species [12]. During drug discovery and development, allometric scaling is a widely used empirical tool for predicting pharmacokinetic parameters of drug products in humans from preclinical animal datasets, especially for the purpose of selecting a safe starting dose for initial clinical trials [13, 14]. Allometric scaling has also be used for interpreting drug-related toxicities such as the maximum tolerated dose (MTD) and therapeutic efficacy across preclinical animal models [15]. The simplest scaling approach uses the power-law function to express an allometric relationship between pharmacokinetic parameters and body weight (Figure 2A). Using a dataset of measured parameters extending over a sufficiently broad range of body weights, one can solve for the allometric function variables (i.e., allometric scaling coefficient and exponent) with type II linear regression of the double-logarithmic transformed datasets (Figure 2B). If the coefficient of determination (R²) of the linear regression is sufficiently high (typically > 0.90 in pharmacokinetic applications), then the allometric function will reasonably predict a drug's pharmacokinetics in untested species via extrapolation.

 Figure 1 

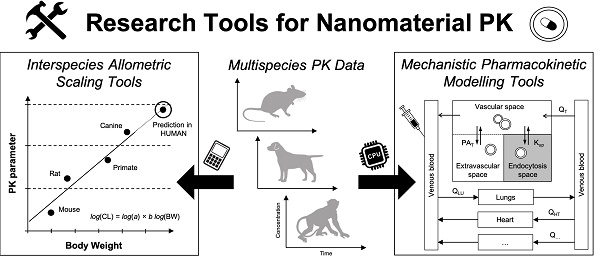
Workflows of two complementary research tools for extrapolating the disposition and pharmacokinetics of nanomaterials from preclinical animals to humans. Left. Interspecies allometric scaling is a tool for extrapolating pharmacokinetic parameters and doses between species on the basis of empirical pharmacokinetic and toxicokinetic data. Right. Mechanistic pharmacokinetic modelling is a tool for predicting the disposition and pharmacokinetics between species on the basis of disposition profiles and physiological data. These two tools as are complementary approaches for understanding and interpreting the disposition and pharmacokinetics profiles of nanomaterials across species, and for extrapolating these profiles accurately in humans.

 Figure 2 

Mathematical representation of the allometric scaling function and relationship across species. A. The simple (or standard) allometric scaling equation based on the power-law function. Modifications to this equation using Mahmood's rule of exponents [36], maximum life-span potential (MLP) or brain weight product scaling, and species-invariant physiological time models (i.e., Dedrick plots) have been investigated for improving allometric relationships of nanomaterial across species. Commonly investigated pharmacokinetic and physiological parameters for nanomaterials are listed in the table underneath. B. Representative double-logarithmic transformation plot of drug clearance versus body weight for mouse, rat, monkey, dog, and man at single equivalent doses (e.g., the MTD in each species). The dotted line originating at 1 kg provides the allometric scaling coefficient a (on the clearance axis) while the slope is determined with linear regression and provides the allometric exponent b. Methods for estimating the scaling exponent from data should use type II linear regressions (e.g., scale invariant total least squares methods) as these account for the variation in both the dependent and independent variables. It is important to note that validation of a genuine power law relationship in log-transformed datasets may require more sophisticated statistics beyond simple evaluation of the goodness of fit using the coefficient of determination (R²). Graphic B adapted from [31].

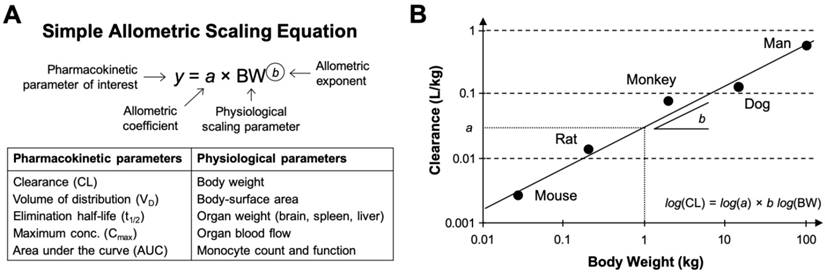
Systemic clearance (CL) is the most commonly scaled parameter from preclinical data using allometry, although the volume of distribution (V_D), area under the curve (AUC), half-life (t_1/2), etc. of nanomaterials can be similarly estimated. Extensive statistical analyses performed on multispecies data from hundreds of small molecule drugs and tens of macromolecule drugs have identified strikingly consistent trends in the allometric function variables. For example, the allometric exponents for predicting the human CL of small molecule drugs (MW < 900 Da) primarily eliminated via renal excretion exhibited significant convergence to the value 0.65 (range 0.65-0.70) [16, 17]. This value is similar to the 0.67 allometric value predicted by the surface area law—a proportional relationship between body-surface area and BMR [18]. On the other hand, analysis of allometric exponents for predicting the human CL of macromolecule drugs and therapeutic proteins (MW between 1-150 kDa) eliminated primarily by extensive hepatic metabolism or in combination with renal excretion, demonstrated central tendencies towards values 0.74 [16] or 0.80 [19], values which are comparable to the 0.734 (rounded to 0.75) value predicted by Brody-Kleiber's quarter-power law theory [20]. Other rules of thumb for estimating the V_D and t_1/2 of small molecule and protein drugs in humans include setting the scaling exponent to 1.0 (range 0.83-1.26) and 0.25 (range: -0.24-0.55), respectively [21]. Although these extensive findings might suggest the existence of a “universal” set of fixed coefficients and exponents for the allometric scaling of drug pharmacokinetic parameters (i.e., on the basis of molecular weight and elimination pathway), this universal approach mindset has been widely criticised as being statistically and empirically invalid [22, 23].

Owing to the lesser number of clinically investigated nanomaterials and the difficulty in obtaining suitable multispecies pharmacokinetic data from literature, statistical analyses of allometric scaling functions and variables for nanomaterial pharmacokinetic parameters has not been possible. There has been extensive research on the influence of isolated physicochemical properties such as composition, shape and morphology, size and aspect ratio, surface chemistry, surface charge, etc. on nanomaterial disposition, pharmacokinetic, and toxicity profiles [24-26]. However, many of these studies suffer from a lack of multispecies data (i.e., data mostly reported in rodent species only), without which correlating the effects of individual nanomaterial properties with biases or trends in allometric relationships are not possible. Ambiguity also exists in these studies regarding how nanomaterial dose should be selected in different species for evaluating the disposition and pharmacokinetics; for example, whether it is more appropriate to select doses on the basis of toxicological findings (e.g., MTD, no-observed adverse effect level (NOAEL)), pharmacological effects (e.g., minimum anticipated biological effect level (MABEL)) or pharmacokinetic observations (e.g., nanomaterial dose threshold for nonlinearity). Studies with small molecule drugs have successfully discriminated the impact of individual physicochemical descriptors on the accuracy of allometric scaling CL in humans [27, 28]. Similar analysis on the basis of individual nanomaterial physicochemical parameters are very limited [29] and may be unfeasible as revealed in the interspecies allometric scaling of PEGylated liposomes: it was discovered that three PEGylated liposomal anticancer drugs with similar physicochemical characteristics exhibited dissimilar allometric coefficients and exponents due to unexpectedly divergent pharmacokinetic profiles, even within the same species and at comparable drug doses [10]. Thus, the available evidence, albeit limited, suggest that even comparable nanomaterials with broadly similar physicochemical characteristics can exhibit dramatic differences in their disposition and pharmacokinetic profiles, which makes generalizations of allometric relationships on the basis of physicochemical descriptors impractical for nanomaterials.

It is noteworthy that many practical applications of simple allometry for extrapolating drug and nanomaterial pharmacokinetics to humans frequently encounter predictive errors because of anatomical, physiological, biochemical, and physicochemical-related factors that cannot scale allometrically with weight [30, 31]. One common explanation for allometric prediction errors of human CLs relates to the challenge of accounting for differences in interspecies hepatic metabolism [30, 32]. Specifically, in the case of drugs with low hepatic extraction ratios (i.e., ratio of hepatic clearance rate to liver blood flow), the intrinsic ability or “capacity” of hepatic enzymes to metabolise a drug greatly determines their systemic clearance in a manner that does not scale allometrically across species [31]. For nanomaterials, additional species-specific differences in the vascular architecture and immune functions of macrophages in the liver and other elimination organs (see Box 1) may result in species-dependent pharmacokinetics profiles for nanomaterial types that are not amendable to allometric assumptions for organism size-dependence. Also, in instances when a drug or nanomaterial's plasma concentration saturates a biotransformation pathway or elimination mechanism—very common for many long-circulating nanomaterial types—the resulting pharmacokinetic profiles may exhibit a nonlinear relationship with dose that is unsuited to allometric scaling approaches [33]. A second challenge for interspecies extrapolation is well documented species-specific differences in protein interactions with drugs and nanomaterials [30]; differences in the strength of binding affinities and in the number of binding sites can restrict glomerular filtration and renal excretion of small-molecule and macromolecule drugs or alter their hepatic metabolism and clearance in a species-dependent manner [34]. Protein binding differences among species likewise have no straightforward allometric scaling with weight. A third limitation of allometry is the necessity for obtaining a sufficiently broad range of species weights for robust correlation; generally greater than three orders of magnitude difference in weights are required, which is at least three or more species of animals [35, 36].

Modifications of simple allometry for improved extrapolation of nanomaterials

Attempts to improve the predictive performance of allometric scaling for the clearance of drugs and nanomaterials include modifications of the standard power-law function with corrections for maximum life-span potential (MLP), in vitro metabolic data (e.g., from liver hepatocyte or microsome assays), protein binding, organ weights (e.g., brain, liver, etc.) and blood flows (e.g., monkey liver), etc. However, some of these modifications have been criticised for being either purely mathematical adjustments without physiological significance (e.g., MLP- or brain weight-corrections, rule of exponents), or for overcompensating hepatic metabolism and biliary elimination pathways (e.g., in vitro metabolism data using the subcellular (microsomes) or cellular (hepatocyte) components of the liver) [30, 31]. Knowing whether and how to apply these corrections appropriately for specific macromolecule drugs and nanomaterials is still unclear, although Mahmood's 'rule of exponents' (ROE) methodology [36, 37] has been successfully applied in published examples of nanomaterial pharmacokinetic allometry. For example, studies with PEGylated anticancer drugs found that using the MLP product scaling of CL (i.e., 8.18 x 10⁵ hours in humans) improved the linear correlation of the allometric scaling function in preclinical animal models [10]. The brain-weight product scaling improved the interspecies linear correlation of PEGylated colloidal gold nanoparticles from R² = 0.957 to 1.000 [38]. Importantly, there is no proven physiological rational for using either MLP or brain-weight product scaling aside from the observation that biochemical processes (i.e., hepatic metabolism) are related to an organism's life expectancy and their evolutionary order.

Generally speaking, the ROE methodology demonstrably improves the predictive power of allometric relationships for drugs and nanomaterials which undergo extensive hepatic metabolism, but has also been criticised for introducing prediction errors in larger preclinical animals (and humans) depending on the species used for fitting [31, 33]. Dedrick plots are a more complex mathematical approach accounting for species differences in physiological time by transforming the time axis of the concentration-time profile from Newtonian chronological time to units of physiological 'species-invariant time' [39]. Upon correcting for physiological time, Dedrick plots of the concentration time profiles of drugs and nanomaterials from different species should be superimposable if bona fide interspecies allometric relationships exists [40]. Dedrick plots of PEGylated liposomal anticancer drugs did not exhibit superimposability and exposed the previously little-known species-dependent characteristics in the disposition and pharmacokinetic profiles of these agents [10]. For other pharmacokinetic parameters, such as AUC, V_D, and t_1/2, consensus over how best to modify the standard allometry function for greater accuracy in humans is still lacking. For instance, attempts to infer t_1/2 in humans from preclinical animal data, as is especially common among nanomaterials reports, are generally poor because t_1/2 is not directly related to a physiological function that conceptually scales with weight [33]. However, since t_1/2 is proportional to the quotient of CL and V_D—both of which are amendable to allometric scaling—and also to the mean residence time (MRT), reasonable predictions of t_1/2 are possible [41]. Nanomaterial AUCs generally scale negatively with body weight since AUC is inversely proportional to CL (itself rarely a negative power with body weight); available evidence for correlating nanomaterial AUCs across species reveals inferior fitting with the allometric power-law function compared with fittings for other pharmacokinetic parameters [42-44].

Examples of allometric scaling of nanomaterial pharmacokinetics across multiple species

PEGylated Liposomes

A pivotal study by Caron et al. in 2012 is among the few to have evaluated with human clinical data interspecies allometric scaling of CL for PEGylated liposomal anticancer drugs (i.e., Doxil, SPI-77 or SPI-077, and S-CKD602) [10]. In addition to simple allometry of CL with body weight, the authors hypothesised that in order to account for the unique physiological role of the MPS in the uptake and disposition of PEGylated liposomes, scaling CL with the weights and blood flows of the liver, spleen, and kidneys, and with the total monocyte count (i.e., number of peripheral blood monocytes per litre of whole blood) may yield more precise predictions in humans. To this end, preclinical animal datasets that included mice, rats, and dogs, each dosed with PEGylated liposomes at their respective MTDs, were analysed. Robust linear regressions were obtained amongst the preclinical animals when the CLs of PEGylated liposomes were scaled by body weight (0.89 < R² < 0.98) and by the total monocyte count (0.93 < R² < 0.99) [10]. However, upon extrapolation to predict CL in humans, the allometric scaling function yielded differences of over 30% (range: -20.4%-698%) from measured values in phase 1 clinical trials [10]. A common challenge in the measurement of plasma concentrations of drug-containing nanomaterials is the difficulty or inability to discriminate the pharmacokinetic profiles of the PEGylated liposomal drug (or nanomaterial) from the free drug; although available evidence suggest that in the PEGylated liposomal drugs studied here the majority (80-95%) of drug in plasma remains encapsulated [45, 46]. Thus, the allometric relationships reported are an accurate description of the PEGylated liposomes themselves.

The discovery that the physiologic properties generating the best scaling of CL across animal models and humans were variables associated with the MPS, such as monocyte count in blood, is highly novel. The conceptual motivation to account for the leading role MPS organs play in the clearance of nanomaterials is attractive, especially as our understanding of the dynamics and mechanisms of nanomaterial clearance in these organs continues to improve [47, 48]. A subsequent study extended upon this theme by establishing allometric associations between the functional activity of circulating blood monocytes (e.g., phagocytosis and radical oxygen species (ROS) production) and the CL of PEGylated liposomes in preclinical animals and humans: the regression fits using the simple power-law function were R² > 0.73 (median: 0.95, max: 0.99) scaled with phagocytosis activity and R² > 0.66 (median: 0.77, max: 0.77) scaled with the level of ROS production [49]. Based on these results the authors proposed a clinical scenario in which surrogate measurements of MPS function via non-invasive phenotypic probes (i.e., phagocytosis and ROS assays) could be used to assess individual oncology patients and predict PEGylated liposome pharmacokinetics, pharmacodynamics (R² > 0.67), and even toxicities (R² = 0.56) prior to the initiation of treatment [49].

Colloidal gold nanoparticles

A fundamental report by investigators at the Nanotechnology Characterization Laboratory outlined in full the clinical development and translation of a colloidal gold nanoparticle platform targeted with tumour necrosis factor-alpha (CYT-6091 or Aurimune), including the interspecies allometric scaling of CL and V_D (data not reported) using approaches developed for macromolecule drugs [38, 50, 51]. Evaluating the disposition and pharmacokinetics of gold nanoparticles is particularly challenging owing to their preferential size-dependent tissue distribution profiles: particles with 10 nm diameters preferentially accumulate in kidney, testis, thymus heart, brain, spleen and liver, while 50 nm particles accumulate primarily in lung, spleen and liver, and particles with diameters greater than 100 nm accumulated in spleen and liver exclusively [52]. On the basis these distribution profiles alone, one cannot predict which sizes of gold nanoparticle will be most (and least) amendable to allometric scaling because the extent to which individual physicochemical properties influence the validity of allometric assumptions still remains unclear. Measuring the pharmacokinetics of their gold nanoparticles with TNF-α levels in the plasma (as opposed to gold concentration, which was deemed technically unfeasible) of rats and rabbits, the authors established an allometric relationship for CL with body weight that was fairly predictive in human (R² > 0.95) [38]. Subsequent modification of the simple allometric equation for CL using brain-weight product scaling recommended in Mahmood's ROE for macromolecules (MW > 100 kDa) [36] dramatically improved the coefficient of determination (R² = 1) of the allometric function; suggesting that the MPS clearance of these nanoparticles possessed a common mechanism in rats, rabbit, and humans [38]. Note however that only two preclinical animal species were used to perform regression of the allometric function, contrary to the recommendations for applying the ROE approach [36]. The successful demonstration of allometric scaling with gold nanoparticles is encouraging for future extrapolation efforts. However it is also possible that had a third animal model (such as dog or non-human primate) been included in the regression analysis as recommended for the ROE approach, extrapolating CL in humans would not have been as accurate (i.e., as experienced by Caron et al. with PEGylated liposomes [10]).

Polymeric nanoparticles

Hrkach et al. reported the clinical translation of a prostate specific membrane antigen (PSMA)-targeted polymeric docetaxel-containing nanoparticle (BIND-014) physicochemically optimised with rational design for superior pharmacokinetics, tissue distribution, and anti-tumour efficacy [43, 53]. Investigating the correlation between nanoparticle/drug dose level and pharmacokinetic parameters in cynomolgus monkeys, the authors obtained a strong linear correlation (R² > 0.99) when comparing the maximum plasma concentration (C_max) and AUC with increasing drug dose levels expressed in body-surface area (i.e., mg of drug per square meter) [43]. Multicycle weekly dosing of their nanoparticles in monkeys exhibited no change in the pharmacokinetic profiles after three administrations; providing clinically-relevant insights on the nanoparticles' pharmacokinetics and MPS-based clearance mechanisms (disposition) upon repeated exposure. Human data from six escalating drug dose levels (3.5 to 75 mg/m²) demonstrated linearly proportional correlations for plasma C_max (R² > 0.87) and AUC (R² > 0.79), similar to results in the monkeys at the same doses. Because of insufficiencies in the data published and the analysis performed, it is difficult to deduce whether a robust interspecies allometric relationship for this nanoparticle's pharmacokinetics truly exists. For example, given the breadth of pharmacokinetic data collected in cynomolgus monkeys and the hepatic elimination (extraction) route of this nanoparticle, it would be interesting to evaluate allometric scaling of CL performed with the monkey liver blood flow approach [28].

Eliasof et al. performed correlative analysis of the pharmacokinetic profiles of a polymeric cyclodextrin-based camptothecin containing nanoparticle (IT-101 or CRLX101) using multispecies animal studies and phase 1 and 2 clinical trial datasets [44]. The authors obtained a strong linear correlation (R² = 0.802) when comparing the plasma AUC of their nanoparticles in rats, dogs, and humans versus increasing drug dose levels expressed in body-surface area (mg/m²) [44], indicating an allometric relationship between CL (inversely proportion to AUC) and dose per meter squared. Interestingly, it was noted that the renal (urinary) excretion process for these nanoparticles became saturated in humans at doses exceeding 15 mg/m², a phenomenon not observed in preclinical animal studies at significantly higher human equivalent doses (~52 mg/m²) [44, 54, 55]. As discussed previously, the saturation of clearance processes not only give rise to nonlinear pharmacokinetic profiles (which cannot be allometrically scaled), but also undermines important assumptions regarding the extrapolation of nanoparticle disposition and pharmacokinetics from animal data [55, 56]. It was also necessary for the authors to account for species-specific differences in the albumin binding affinity for camptothecin (which also cannot be allometrically scaled) to improve the consistency of the pharmacokinetic profiles across species [44]. Regardless, it is interesting to note how failure to anticipate minor species-specific effects in renal excretion and protein binding during preclinical testing of this nanomaterial diminished the predictive power of allometric scaling AUC in patients.

Investigating a related cyclodextrin-based targeted nanoparticle containing small interfering ribonucleic acid (siRNA) (CALAA-01), Zuckerman et al. reported linear relationships between plasma siRNA pharmacokinetics (AUC and C_max) and nanoparticle dose (mg/m²) in rats, cynomolgus monkeys, and humans (R² > 0.9) [57, 58]. Curiously, whereas Eliasof et al. had found the AUC of their cyclodextrin nanoparticles scaled best with body-surface area [44]—as one would anticipate from evidence with renally eliminated macromolecule drugs—Zuckerman et al. found superior correlation of C_max among mice, rats, dogs, monkeys, and humans (R² > 0.98) when dose was expressed in body weight (mg/kg) [57, 59]. This finding is not unexpected considering that aside from the shared route of clearance (renal excretion), the physicochemical characteristics between these two cyclodextrin-based nanoparticles are broadly dissimilar and contribute to significant divergence in their respective pharmacokinetic profiles. Furthermore, scaling pharmacokinetic parameters and dose on the basis of body weight is recommended in instances when a drug or nanomaterial's C_max correlates across preclinical species with mg/kg, which is indeed the case with CALAA-01 [30, 57-59]. Importantly, the rapid renal clearance of CALAA-01 (t_1/2 ~15 minutes), although creating technical difficulties for assessing the AUC, CL, and t_1/2, does not necessarily invalidate the allometric relationship established for C_max [57]: predominantly excreted (but not secreted) drugs are still amendable to allometric scaling of their CL and may even be improved with scaling corrections for GFR or the number of nephrons (both of which scale allometrically) [30].

Outstanding challenges for scaling nanomaterial pharmacokinetics

The examples of allometric scaling discussed above provide confidence and optimism in the predictive utility and accuracy of extrapolative tools for nanomaterials. However, the available evidence are still insufficient for advising on a generalizable strategy for conducting allometric extrapolation of pharmacokinetic parameters or dose, particularly on the basis of a nanomaterial's physicochemical properties. In order for such as strategy to take shape, allometric scaling approaches will need to be refined in order to better capture defining characteristics of nanomaterial behaviours in vivo. For example, how to account for information of a nanomaterial's protein corona in allometric scaling? The protein corona has an outsized effect on the disposition and pharmacokinetic profiles, such as restricting the access and distribution of nanomaterials to their sites of action and excretion (e.g., preventing the diffusion across barrier membranes in the kidney glomerulus). Whereas many small-molecule drugs possess well defined interactions with plasma proteins that can be rationally accounted for in the allometric function, hundreds of proteins have been identified in the time-varying coronas of intravenous nanomaterials [60, 61]. Our understanding of the thermodynamics and stoichiometry of protein corona formation [62] and their influences the disposition and tissue uptake of nanomaterials continues to evolve [63, 64]. However, available evidence suggests that the kinetics and dynamics of corona formation on nanomaterials is mostly independent of physiological rates (e.g., BMR), which makes simple extrapolation with body weight theoretically problematic [65].

Differences in the time scales on which physiological and metabolic processes (e.g., BMR) occur versus protein corona formation kinetics create mismatches that have been hypothesised to contribute to significant differences in the distribution profiles of nanomaterials extrapolated between species. For example, in silico modelling has revealed that rapidly forming (e.g., minutes) stable protein coronas will have minimal impact on extrapolations of nanomaterial distribution, while coronas requiring hours to reach a stable form (>> BMR time scale) could impart dramatic differences in distribution across species [63]. Lastly, interspecies differences in the blood proteomes and the resulting compositions of protein coronas may further confound extrapolation efforts [65]. Studies comparing the protein coronas formed on liposomes of varying physicochemical characteristics in the plasma of mice and humans revealed significant differences in the densities and types of proteins bound to the surface of the liposomes [66, 67], differences which could lead to species-dependent disposition. Therefore, overcoming the effects of protein corona with simple arithmetic modifications to the allometric power-law function seems unlikely; the best strategies described to date combines experimental in vitro and in vivo data and in silico modelling approaches for aid extrapolation methods [63].

A second obstacle for the allometric scaling of nanomaterials is the nonlinear or dose-independent disposition and pharmacokinetic profiles (e.g., distribution, elimination, etc.) typical of many intravenous long circulation nanomaterials. There is no conceptual basis for scaling nonlinear pharmacokinetic parameters with allometry since these parameters (response variables) will exhibit relationships with multiple explanatory or independent variables (i.e., body-weight, dose, etc.) that can only be fitted with multiple linear regression analysis (not a power-law function). Nonlinearity usually arises from the saturation of elimination mechanisms associated with MPS organs, such as phagocytic Kupffer cells in the context of intravenous nanomaterials eliminated by the liver [6, 48]. A similar phenomenon arises with clinical monoclonal antibodies in vivo: antibodies exhibit significant dose-dependent pharmacokinetics and elimination (i.e., usually via receptor-mediated endocytosis in the liver, vascular endothelium, or target tissues) where clearance decreases as a function of dose upon exceeding receptor capacity [68]. Predicting with allometric extrapolation the dose wherein nonlinear, target-mediated disposition of antibodies in humans begins is often unsuccessful [68]. Similar attempts at predicting nanomaterial pharmacokinetic nonlinearity between preclinical models and in humans have been unsuccess as well. For example, polymeric nanoparticle CRLX101 saturated the renal elimination pathway in humans at a significantly lower dose than predicted from the allometric relationship using preclinical animal models (15 mg/m² versus ~52 mg/m²) [44]. In this instance, allometric scaling of the preclinical dose with a more appropriate physiological parameter reflective of the nanomaterial's renal excretion (e.g., GFR, kidney blood flow, number of nephrons, etc.) might have better predicted nonlinearity in humans.

The classical properties associated of nanomaterials such as prolonged circulation times, moderate distribution into tissues, and predominant interactions with the MPS and clearance organs—which can species-specific and size-independent (see Box 1)—all work against deriving predictive allometric relationships for CL and dose across species. The clinical implication of this fact has already been described: in initial clinical trials with nanoparticles, the ratio of the MTD to starting dose in patients was approximately 7-fold higher, a statistically significant difference in comparison with similarly designed small molecule drug trials [11]. This finding suggests that the starting nanoparticle dose extrapolated with allometry from preclinical animal models used for toxicity testing (mainly rats and beagle dogs) were poorly predictive of the MTDs in humans. Importantly, the starting doses for the nanoparticles reviewed in this study were calculated from the most sensitive species on a mg/m² basis using a conventional dose-by-factor approach, which may not be an ideal approach for nanomaterials [38]. For nanomaterials that share physicochemical characteristics and disposition profiles with therapeutic protein drugs, specifically in terms of their molecular weight (MW > 100 kDa), low metabolism, and distribution primarily into the plasma space, it has been suggested that scaling dose directly with body weight (mg/kg) may provide better estimates the safe starting doses in patients [30, 38]. Regardless of the approach employed, the consequences of starting patients on too low or conservative a dose in initial clinical trials is that the majority of patients in these trials will be treated at doses that are unlikely to produce toxicity and/or therapeutic response, thereby undermining the purpose of in human safety studies [11].

Leveraging allometric relationships to estimate clinical starting dose

The predicted disposition and pharmacokinetic profiles of nanomaterials in humans are important for anticipating dose-dependent exposure-pharmacodynamic response relationships and for establishing the MRSD for initial clinical trials. However, there is no consensus on the best method for selecting a first dose for nanomaterials in humans. Regulatory guidelines from the United States Food and Drug Administration (USFDA) recommend a dose-by-factor approach wherein the NOAEL of a drug in the most sensitive preclinical species is scaled by using simple allometry on the basis of body-surface area (allometric exponent b = 0.67) to obtain the human-equivalent dose (HED) (Figure 3A) [30, 38]. The HED is next divided by a safety factor with default value 10, although this value does not have a firm scientific basis and is purely cautionary. This approach has a good safety record for nanomaterials because it is very conservative [11], and its simplicity to apply makes it attractive to scientific and clinical investigators. The selection of the appropriate test species for performing NOAEL studies is an important decision since the appearance of toxicities or adverse effects to nanomaterials can arise from numerous physiologic, biochemical, metabolic, and pharmacologic processes that may vary greatly across species [8]. The appropriateness of a test species can be evaluated on the basis of expectant similarities in the ADME of a nanomaterial to humans and from prior experiences assessing the toxicity of nanomaterial types in a particular species [69]. It has been suggested that nanomaterials can be scaled on the basis of mg/kg (allometric exponent b = 1) directly from the most sensitive species when either (i) the NOAEL among species on a mg/kg basis are highly similar or (ii) the C_max is the primary determinant of toxicity and is strongly correlated with dose (mg/kg) [38]. However, dose conversion based on mg/m² is still widely favoured for it's more conservative dose estimate, especially for first-in-class nanomaterials.

 Figure 3 

Allometric scaling approaches for estimating the dose and systemic clearance of nanomaterials. A. Current methods for dose estimation of the maximum recommended starting dose (MRSD) in initial clinical trials and of the animal-equivalent dose (AED) for experimental studies (i.e., human therapeutic dose equivalent in preclinical animal models). All these approaches rely on allometric scaling either of the nanomaterial dose (mg/kg) itself or of the nanomaterial clearance (CL) using preclinical pharmacokinetic data. A default safety factor of 10 is applied in the calculation of the MRSD from the human-equivalent dose (HED). A key limitation of these approaches is the extent to which the pharmacokinetic and toxicologic parameters of the nanomaterial can be accurately predicted in humans with allometry, which for most nanomaterial types is not always guaranteed. Information in A adapted from [30, 71]. B. Decision tree for selecting the recommended allometric scaling method of nanomaterial CL on the basis of their clearance/elimination route. These recommendations and the additional considerations are based on the best practices for interspecies scaling of nanomaterial CL reported in literature. It is not meant as a prescriptive tool. Whether or not a particular nanomaterial type is amendable to allometric scaling will ultimately depend on the multispecies experimental data.

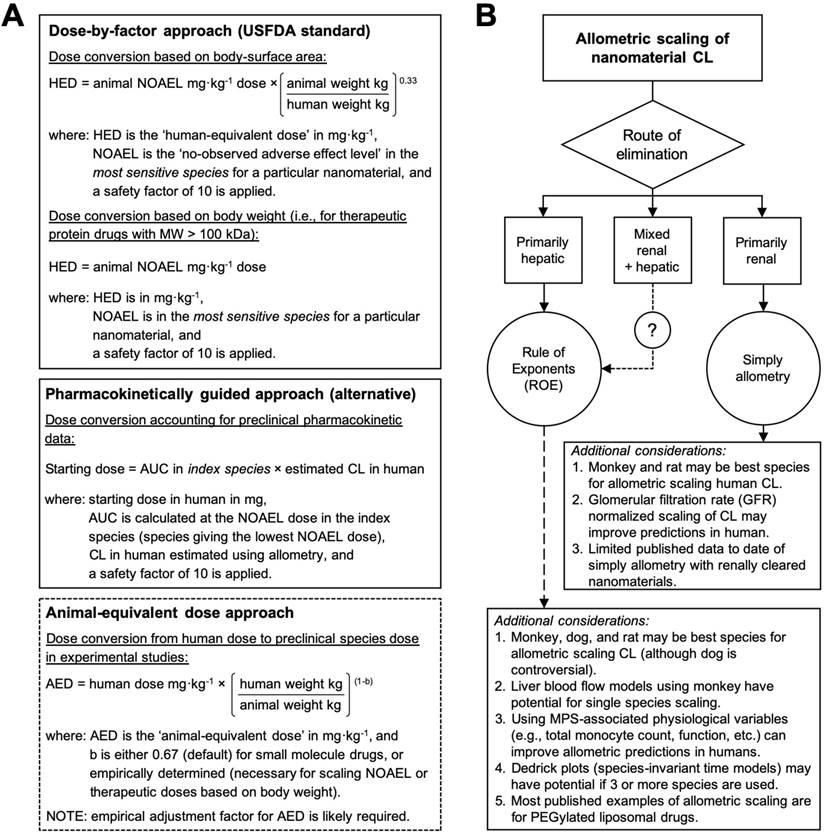
A key limitation of the dose-by-factor approach is the lack of account for preclinical pharmacokinetic data in the calculation (i.e., only the NOAEL is required), usually leading to underestimations of the effective dose and necessitating greater time, cost, patient numbers and dose escalations in order to find the therapeutic range and demonstrate therapeutic efficacy [11]. Alternative approaches to dose extrapolation, such as the pharmacokinetically guided approach, aim to better estimate safe starting doses using systemic exposure (a primary determinant of toxicity [70]) and empirical allometric relationships for CL and/or V_D [30, 38]. In this approach, the NOAEL is determined in several test species, and the species that gives the lowest NOAEL is used as the index species for calculating AUC and scaling CL or V_D in humans (Figure 3A). Curiously, studies comparing the pharmacokinetically guided approach with the conventional dose-by-factor approach for small-molecule drugs reported insignificant differences in the prediction of the recommended (therapeutic) dose between the two approaches [71, 72]—most likely because across species variations in the CL and V_D are higher than variations in the NOAEL (mg/m²). Thus, a key limitation of the pharmacokinetically guided approach is the extent to which the pharmacokinetic parameters of a nanomaterial can be accurately predicted in humans, which for most nanomaterial types is not always guaranteed. Another caveat for this approach is that the AUCs of nanomaterials generally scale negatively with body weight, and if the NOAELs among the species are similar, significant differences in the MRSD can be calculated depending the species selected for indexing and scaling. Therefore, the best strategy for selecting the clinical starting dose includes using both the dose-by-factor and the pharmacokinetically guided approaches to derive several candidate doses that can then be critically assessed for their relative merits and drawbacks [30, 71].

Summary of allometric scaling tools for extrapolating preclinical nanomaterial pharmacokinetics and doses in humans

Published examples of allometric scaling nanomaterial pharmacokinetics and dose in humans remains surprisingly limited, especially in light of the over sixty early phase clinical trial currently being conducted with nanomaterials in the United States alone. The available evidence suggest that the classical properties associated of many nanomaterial types, such as prolonged circulation times and nonlinear pharmacokinetic profiles, protein corona formation, and extensive interactions with the MPS organs (particularly the liver), all work against deriving predictive allometric relationships across species. Furthermore, the diversity of physicochemical properties and pharmacokinetic profiles manifested by nanomaterials make it is unlikely that a single allometric scaling approach will work for all nanomaterial types equally. Rather, consolidating the available evidence for scaling nanomaterial pharmacokinetic parameters highlights general trends in the extrapolation methods most likely to succeed: on the basis of elimination route, for example (Figure 3B). The best strategies for allometric scaling will include testing multiple extrapolation methods and then critically assessing each relationship for their relative merits and drawbacks. Whether or not a particular nanomaterial is amendable to allometric scaling will ultimately depend on the multispecies pharmacokinetic data.

Overall, the following can be concluded from allometric scaling of preclinical nanomaterial pharmacokinetics and dose in humans:

• There are no universal set of allometric coefficients and exponents for scaling nanomaterial pharmacokinetics across species. Nor does the available evidence suggest a central tendency will emerge in the exponent values dependent on the route of elimination—such as 0.67 for renally excreted small molecule drugs or 0.75 for hepatically metabolised small molecule and macromolecule drugs, for example.
• The most predictive allometric scaling relationships for nanomaterials are regressed with pharmacokinetic data from at least 3 species of animals (or 3 orders of magnitude weight difference). The selection of appropriate test species for studying nanomaterial pharmacokinetics and toxicokinetics is not trivial [8, 9, 69] and will depend on similarities in the nanomaterial disposition (ADME) to humans and on prior experiences in a particular species with a given nanomaterial type.
• The inclusion of variables associated with the MPS in allometric scaling approaches have an appealing conceptual basis, especially when analysing nanomaterial with primary elimination through MPS-associated organs like the liver and spleen. However, it is still unclear to what extent nanomaterial MPS sequestration scales across species with body weight or any other physiological parameter.
• Size-independent species differences that affect nanomaterial disposition and pharmacokinetic profiles are not amendable to allometric scaling. These include differences in hepatic enzymes and enzymatic pathways (affecting metabolism), in the physiology and function of the MPS and clearance organs (affecting elimination), and in the blood proteome (affecting protein corona).
• Nanomaterial physicochemical properties that are intended to alter their distribution in vivo (e.g., targeted nanomaterials), that may promote extensive hepatic clearance and biliary excretion (e.g., large and amphiphilic components), or that impart nonlinear disposition and pharmacokinetic profiles (e.g., PEGylated nanomaterials) are all unlikely to be amendable to allometric scaling.

Box 1. Species-specific differences in the mononuclear phagocytic system (MPS) organs and their influences on nanomaterial disposition and pharmacokinetics.

MPS uptake in macrophage rich organs, such as the liver and spleen [73], are classical features of most long-circulating and nondeformable nanomaterials [74]. Differences in the types and relative abundance of phagocytosing cells among the various MPS organs are well understood, as are the physicochemical properties of nanomaterials generally affecting protein opsonization and MPS uptake [9]. What is less appreciated are the differences among preclinical species in the anatomical architecture of MPS vascular systems and the immune function of macrophages. These species-specific variations can result in distinct microcirculatory pathways and different mechanisms of blood clearance that may have meaningful consequences for the interpretation and extrapolation of nanomaterial disposition and pharmacokinetic profiles across species.

Spleen. The mouse spleen capillary is non-sinusoidal with predominant blood flow through open-circulation routes where nanomaterial filtration is primarily regulated by the function of barrier cells [75]. In rats and humans, the spleen capillary is sinusoidal, where most of the blood flows through the open-circulation route with filtration at interendothelial cell slits [75]. A study of comparing the intrasplenic distribution of polystyrene nanospheres in mice and rats reported dissimilar distribution patterns [76]. In mice, most of the injected nanospheres (~140-200 nm dia.) were localised in the marginal zone, involving a special population of antigen capturing marginal zone B cells [77], whereas in rats the predominant capture of these nanospheres occurred in the red pulp. When the properties of the nanospheres were adjusted with a hydrophilic coating (~200-220 nm diameter, ~0 mV surface charge) the intrasplenic distribution of capture in mice shifted to the red pulp, presumably due to changes in the opsonic response to the hydrophilic coatings that affected the specific cellular interactions with the nanospheres [76, 78]. In the sinusoidal structures of rat and human livers (but not mice), the splenic interendothelial cell slits (200-500 nm) in the walls of venous sinuses act as a sieving mechanism for entrapping and accumulating nondeformable nanomaterials of equal or greater sizes in the red pulp [78, 79]. The relationships between nanomaterial properties and splenic accumulation across different species has been reviewed in depth elsewhere [74].

Liver. The liver capillaries of mice, rats, and humans are all sinusoidal with open endothelial fenestrae separating the sinusoidal lumen and the space of Disses where the hepatic parenchymal cells (hepatocytes) reside. However, the number of fenestrae per μm² and the diameters differs among species: the average diameter of fenestrae is ~99 nm in mice and rats, but is between 50-300 nm in humans, and the density of fenestrae/μm² is 14, 20, and 20 in mice, rats, and humans, respectively [80]. The influences of these anatomical differences on the intrahepatic distribution and hepatobiliary clearance of nanomaterials between species has not be studied in depth. Reports on the species dependent hepatic uptake of liposomes in mice, rats, and rabbits noted that liposome uptake in rats was dependent on specific plasma opsonins whereas mice exhibited opsonin independent uptake [81, 82]. Although, species specificity has also been reported in the activity of particular opsonins against liposomes too [82]. No significant differences have been observed in the density of Kupffer cells in mouse, rat, and rabbit livers [81]. More multispecies data, specifically in nonrodent species and humans, are needed in order to conclude which preclinical animal models can best recreate nanomaterial intrahepatic distribution, hepatobiliary clearance profiles, and hepatotoxicity in humans. The relationships between nanomaterial properties and hepatic accumulation have been reviewed in depth elsewhere [48, 74].

Bone marrow. Anatomical differences in the bone marrow across species have been observed. A report on interspecies differences in the accumulation of chylomicrons in the bone marrow found higher uptake of these nanoparticles in the marrow perisinusoidal macrophages of rabbits and marmosets, but not in rats, guinea pigs, and dogs [83]. It was observed that in rabbits and marmosets, macrophages processes protruded through the sinusoidal endothelium into the marrow sinus; data from other species were not reported [83].

Lungs. Pulmonary alveolar macrophages, which adhere to the capillary endothelium of the alveoli (i.e., exposed to blood stream) and are primarily implicated in the clearance of inhaled nanomaterials, are reportedly larger and have superior phagocytic capability in humans as compared to rodents, dogs, or non-human primate species [9]. Another population of giant phagocytosing cells (20-80 μm) identified in the lungs of pigs and sheep, and capable of clearing nanomaterials within minutes of intravenous administration are known as pulmonary intravascular macrophages [84-86]. These cells elicit a tachyphylaxitic complement activation-related pseudo-allergy (CARPA) in pigs upon exposure to nanoparticles, leading to the rapid onset of cardiorespiratory symptoms (e.g., pulmonary vasoconstriction, bronchoconstriction, and pulmonary hypertension) similar to infusion reactions observed in clinical patients with PEGylated liposomal anticancer drugs [69, 86]. Although these macrophages are not present in the lungs of other preclinical animal models (i.e., mice, rats, dogs) or humans under physiological conditions, evidence suggest that they can be induced in the lungs of rodents and humans under certain disease states, such as sepsis, liver cirrhosis, and numerous intrapulmonary pathologies [87]. Thus in the context of infusion reactions towards nanomaterials, Szebeni et al. have hypothesised “hepatopulmonary macrophage migration” in humans wherein activated liver and spleen resident macrophages are induced to migrate to the lungs during an infusion, triggering cardiorespiratory symptoms in a similar manner to pulmonary intravascular macrophages [69]. This hypothesis has yet to be verified experimentally.

Kidneys. Renal physiology exhibits good allometric relationships with body weight [12]. Anatomical differences in the relative number of nephrons per gram of kidney tissue are higher in small animals than in humans [88]. There have been no noteworthy species differences reported in the vascular architecture and immunological function of the kidneys related to the elimination (renal excretion) of nanomaterials [89].

Mechanistic modelling of nanomaterial disposition and pharmacokinetics in humans with physiologically-based methodologies

An introduction to mechanistic modelling tools of pharmacokinetics

The most frequently reported mathematic models for analysing nanomaterial pharmacokinetics are either empirical (e.g., sum of exponential terms) or compartmental (e.g., one- or two-compartment models) (Figure 4A). These models provide simple mathematical descriptions of experimental concentration-time profile data with the fewest assumptions for the physiological systems surrounding the data—making them both computationally simple and helpful for describing and interpolating pharmacokinetic data. However, the lack of physiological meaning in the compartmental and/or parametric relationships these models describe creates challenges when trying to extrapolate existing pharmacokinetic profiles to different species or for different doses, for example [90]. To address this extrapolation issue, mechanistic modelling approaches are preferred since they seek to integrate information about the biological and physiological processes that underlie nanomaterial disposition and pharmacokinetics into the model assumptions and mathematical descriptions (equations) of experimental data. Thus, these models can simulate new pharmacokinetic profiles with discrete changes in the model assumptions and variables, and without requiring entirely new experimental data.

 Figure 4 

Empirical versus mechanistic pharmacokinetic modelling approaches. A. An example of a two-compartment model parameterised in micro-rate constants k₁₂ and k₂₁ (distribution rates between central and peripheral compartments) and k₁₀ (clearance rate from central compartment). Two-compartment models provide simple mathematical descriptions of experimental concentration-time profile data with the fewest assumptions for the physiological systems surrounding the data—making them both computationally simple and helpful for describing and interpolating pharmacokinetic data. B. An example of a whole body physiologically base pharmacokinetic model (WBPBPK) where compartments represent actual tissues and organs arranged anatomically. Connecting arrows represent blood supplies and elimination processes can be attributed to some organs (e.g. liver and kidney, dotted arrows). Various routes of administration can be represented (intravenous and per os illustrated here). The model depicted here can be extended (empty box at the bottom) to incorporate additional organs. These models can simulate new pharmacokinetic profiles with discrete changes in the model assumptions and without requiring new experimental data. Graphics adapted from [31].

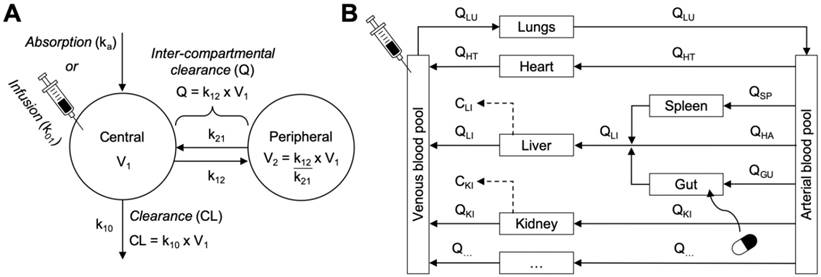
Physiologically based pharmacokinetic (PBPK) methodologies are an example of mechanistic modelling wherein the disposition and pharmacokinetics of a nanomaterial are described by their mass transport between individual compartments representing real anatomical structures and interconnected by blood flow (Figure 4B). These models describe pharmacokinetic behaviours in relation to blood flows, tissue volumes, routes of administration, biotransformation pathways, and interactions with organs, tissues, and cells [31]. Within each compartment, kinetic processes like diffusion and convection, membrane permeability, protein binding, transport kinetics and metabolism can be included based on species-specific and drug-specific input parameters. The steps for designing a PBPK model specific for simulating nanomaterial disposition and pharmacokinetics are detailed in Box 2. The key advantage of these models is that by accounting for the critical physiological characteristics and biological determinants of nanomaterial disposition and uptake, extrapolation for dose-response and organ exposure can be performed more accurately and under several physiological conditions (e.g., different species, disease states, routes of administration, etc.). Thus, PBPK models can be powerful quantitative tool for understanding and predicting the therapeutic efficacy and toxicity hazards of nanomaterials during the discovery and development phases.

Modifications of PBPK frameworks to model MPS organ uptake of nanomaterials

Perhaps the most critical transportation mechanism in the context of many intravenous nanomaterials is uptake in MPS organs: liver, spleen, kidneys, lungs, lymph nodes and bone marrow. The distribution of nanomaterials to these organs is well documented and our collective knowledge of the physicochemical, physiological and biological determinants of nanomaterial interactions with MPS organs is steadily growing [48, 74, 91, 92]. However, the inclusion of MPS uptake in PBPK models is not always straight forward since the endocytosis kinetics are likely both concentration- and time-dependent, for which fixed model parameters cannot accurately portray. One simple solution is to incorporate rate equations for describing nanomaterial transport into the tissue compartment as concentration-dependent, saturable uptake mechanisms (i.e., using a non-Michaelis-Menten type function of negative cooperativity) [93]. Saturation-based mechanism models have proved superior to the linear (or fixed parameter) uptake mechanism when fitted to experimental preclinical and clinical datasets [93]. More recent approaches have included separate representations of endocytosis and related cellular uptake processes (e.g., “profession” endocytosis or phagocytosis) as saturable, permeability rate-limited sub-compartments in the MPS organs (Figure 5). These approaches have been implemented for modelling intravenously administered PEGylated polyacrylamide (PAA) nanomaterials [94], PEGylated gold nanomaterials of varying size [95, 96], and gold nanorods and titanium dioxide nanomaterials [97]. The model parameters commonly used for describing the kinetics of cellular endocytosis include the maximum uptake capacity and uptake rate, which are determined either mathematically during model optimisation or, preferably, from in vitro in vivo extrapolation studies with tissue-specific macrophages.

 Figure 5 

Modifications to PBPK frameworks for nanomaterials with MPS uptake. Options for representing the cellular endocytosis/uptake of nanomaterials in permeability rate limited compartments. The endocytosis of nanomaterials can occur either directly from capillary blood (i.e., by endothelial cells or macrophages directly lining the capillary walls) (A), by macrophages in the tissue (B), or in the lymph (C). Selection of the appropriate representation for cellular endocytosis will depend on the nanomaterial type (e.g., predominantly nanomaterial size dependent) and the availability of experimental distribution data. The Hill equation is shown here for modelling the nonlinear time-dependent (as in A) or concentration-dependent (as in B) uptake rate (K_up) of nanomaterials into the endocytosis compartment (tissue specific) [95]. Physiological parameters (e.g., blood flows, tissue volumes, etc.) are nanomaterial independent and can usually be retrieved from literature. Physicochemical- and biochemical-related model parameters (e.g., tissue-to-plasma distribution coefficient (Kp_T:bl), tissue permeability-surface area product (PA_T), endocytosis velocity (k_max) and half-maximal constant (k₅₀), etc.) are nanomaterial dependent and must be determined either by estimation from data-fitting or empirically from in vitro to in vivo extrapolation studies. The complex convectional (or cyclical) transportation of nanomaterials between the lymphatic system and tissue interstitial space, and the blood circulation are illustrated in C. Graphics and equations for A and B adapted from [31, 95].

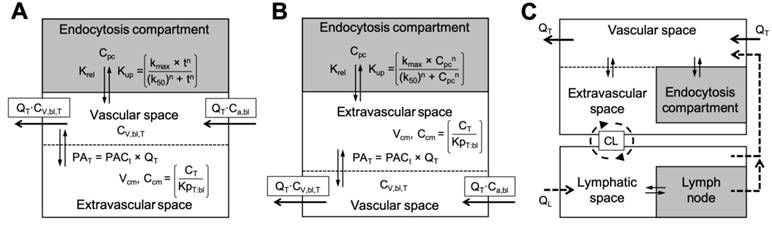
Special consideration for the orientation of nanomaterial flux (rate functions) into the endocytic sub-compartment is required since phagocytosis of nanomaterials has been described occurring either directly from the blood (i.e., by endothelial cells or macrophages directly lining the capillary walls), by macrophages in the tissue, or from the lymph (Figure 5) [95, 98]. For example, PBPK model simulations for smaller sized nanomaterials (e.g., 13 nm to 35 nm) perform better when cellular endocytosis is limited to within tissues (Figure 5B), whereas larger nanomaterials (e.g., > 100 nm) are better simulated by endocytosis occurring directly from the blood (Figure 5A) [94, 95]. Models implementing endocytosis-related mechanisms have reported excellent regression coefficient (R² > 0.97) between the model simulated and measured data when species-specific endocytosis-related parameters are known [96]. Although these improvements provide more accurate physiological descriptions of nanomaterial pharmacokinetics, especially in the MPS organs, most models still simplify endocytic transportation to a single common that does not account of the complex roles of physicochemical properties, protein corona, and phagocytotic differences between organs (e.g., cell type, density) and between species (detailed in Box 1). These differences should be more rigorously considered in future PBPK frameworks, especially for applications in extrapolating nanomaterials demonstrating significant clearance/elimination by MPS uptake in humans.

Examples of PBPK modelling applications for nanomaterials

Rational design of nanomaterials

One of the first practical demonstrations with whole body PBPK modelling with nanomaterials was for studying quantitative relationships between specific physicochemical properties (e.g., size, surface chemistry and charge, etc.) and observed or simulated ADME profiles [99]. Working with pharmacokinetic data from intravenously administered PEGylated poly(lactic-co-glycolic acid) (PLGA) nanomaterials with varying methoxypolyethylene glycol (mPEG) contents in mice, the authors identified good linear and nonlinear relationships between model parameters describing biodistribution kinetics (i.e., diffusion, tissue-to-blood partition, and excretion coefficients) and individual physicochemical properties (i.e., size, surface charge, and mPEG content). These relationships were then used to estimate the parameters of an independent PLGA-mPEG nanomaterial based on its physicochemical properties, where upon simulation with in PBPK model yielded biodistribution estimates that closely agreed with experimental data. A similar studyhasalso been performed with poly(amidoamine) (PAMAM) dendrimer-colloidal gold composite nanodevices of varying sizes and surface charges [100]. It is important to note that leveraging PBPK modelling to establish quantitative property-ADME profile relationships does not overcome the key limitation of rational design approaches: that is, the relationships established cannot be generalised across all nanomaterial types, but rather are descriptive of only nano materials with highly similar physicochemical properties and pharmacokinetic profiles.

Generalizable PBPK models for multiple nanomaterial type

Carlander et al. reported the development of a PBPK modelling platform intended for describing the biokinetic profiles of intravenous nanomaterials with diverse physicochemical properties and disposition profiles [97]. The authors modified an existing PBPK model [94] by incorporating a common saturable endocytosis sub-compartment and mechanism in all organs; a design feature emphasised as a critical for ensuring the generalisability of their model for intravenous nanomaterial biokinetics. However, this oversimplification of nanomaterial phagocytosis to a single mechanism overlooks studied differences in the pathways and uptake capacities of endocytosis cells, which can depend greatly on physicochemical properties and may be highly heterogenous across nanomaterial types [26]. After optimising for nanomaterial-dependent (i.e., tissue-blood permeability coefficient) and endocytosis-related (i.e., maximal phagocytosis capacity) model parameters for four different nanomaterial types, the authors obtained adequate correlations between the model simulated and experimental distribution data: R² ranged between 0.88 (gold nanorods), 0.91 (titanium dioxide), 0.94 (polyacrylic acid) and 0.96 (PEG-polyacrylic acid) [97]. Unsurprisingly, the authors found large differences amongst the sets of optimised model parameters with each nanomaterial type. For instance, 100-fold extreme differences were observed for the rate of phagocytotic uptake, maximal phagocytotic capacity, and plasma half-life between nanomaterials (primarily between inorganic nanoparticles and organic nanoparticles) [97]. A unique finding that emerged during the model optimisation step was the vulnerability of estimating endocytosis-related parameters using only a single nanomaterial dose [97]. The high sensitivity coefficients of the simulations to dose highlights important considerations for optimising PBPK model parameters with biokinetic data from multiple dose levels, especially in cases where the pharmacokinetic profile exhibits dose-dependencies (or nonlinearity). Future efforts for fully generalisable nanomaterial PBPK models will require more thorough investigation and integration of quantitative relationships between properties and biokinetics for multiple nanomaterials types and properties, and at multiple doses in multiple animal species.

Extrapolating nanomaterial pharmacokinetics in humans with PBPK modelling

The most sophisticated demonstration of nanomaterial biokinetic and pharmacokinetic profile extrapolation in humans with PBPK modelling was a computational framework developed by Lin et al. for gold nanomaterials [96]. In theory, extrapolation of a validated preclinical PBPK model to humans should be as simple as altering the physiological parameters to be human-specific while keeping nanomaterial- and endocytosis-related parameters similar to their optimised preclinical values. However, upon performing extrapolation in this manner using mouse, rat, and pig specific models, the authors discovered that the simulated data of gold distribution in humans inadequately matched observations (R² < 0.87) [96]. Revising the endocytosis-related model parameters to either account for interspecies differences in densities of liver Kupffer cells (pig model) or for empirical differences in dose-dependent biokinetics (rat model), improved the correlation of the simulated human data to R² > 0.93 [96]. The discovery that the revised models developed for gold nanomaterial specifically in rats and pigs yielded superior animal-to-human extrapolation is highly novel. It was hypothesised that anatomical, physiological, and immunological similarities of phagocytosing cells in the MPS organs of rats, pigs, and humans (but not mice) resulted in the improved correlation with human data following revision [96]. Comparison of many common physiological parameters (e.g., cardiac output, blood volume fraction in liver or spleen, etc.) reveals further closeness between pigs and humans, while mice generally exhibit 3-fold differences from humans [95]. Thus, this study highlights once more the importance of selecting appropriate animal models with physiological likeness to humans for collecting biokinetic data used to optimise and validate mechanistic PBPK models, failure of which leads to inaccurate extrapolations of nanomaterial disposition (ADME) and pharmacokinetics in humans.

PBPK-based approaches for extrapolating nanomaterial toxicity in humans

There is a growing appreciation for the potential role of PBPK modelling to guide nanomaterial discovery and development with accurate predictions of organ exposure and dose-response profiles in humans. However, predicting toxicities and adverse events in humans ex nihilo remains limited since the mechanisms of toxicities on the scale of an entire living organism are often complex and unanticipated. Rather, the PBPK framework can be used best to generate insightful hypotheses for nanomaterial toxicokinetic and toxicologic profiles. For example, the sequestration of nanomaterials in the phagocytosing cellular populations of tissues is highly informative for predicting the efficacy and toxicologic risks associated with their disposition. Sequestration may be beneficial for avoiding direct toxicities and damage to healthy tissue cells (e.g., sequestrations in Kupffer cells prevent hepatotoxicity [48]). Conversely, the desorption of nanomaterials, especially the nondegradable variety, from phagocytosing cells back into surrounding tissues over time can extend organ exposure long after the majority of the dose has been eliminated. For nanomaterials with drug delivery functions, consideration for the intended pharmacological effects of the drug needs to account for reduced delivery to target cells whilst the nanomaterial remains captured in phagocytosing cells.

The mechanistic nature of PBPK frameworks make them easily amendable to incorporating experimental toxicologic data from in vitro in vivo extrapolation (IVIVE) studies or from toxicity studies in multiple species, such as NOAELs and MTDs. One study described the extrapolation of gold nanoparticle toxicities to humans using multispecies in vitro and in vivo toxicity data and PBPK modelling, successfully estimating the associated human equivalent dose (HED) of nanoparticles for cytotoxicity, and hepatic and haemolytic toxicities [96]. Another study sought to model the formation of anti-PEG antibodies to PEGylated drugs in mice and humans using a minimal two-compartment PBPK framework [101]. Specifically, the model included physiological parameters describing antibody behaviours (e.g., production, stimulation and elimination, diffusion, etc.) and the opsonisation kinetics to PEGylated drugs, and was validated with pharmacokinetic data of PEGylated liposomes exhibiting antibody-mediated accelerated blood clearance in mice. The authors reported accurate simulations not only of clinical pharmacokinetic behaviours of antibody-mediated clearance and memory response to multicycle doses of PEGylated liposomes, but also estimated in humans the concentration of antibodies needed (~500 ng/mL) to elicit an accelerated blood clearance effect [101]. These two examples speak to the promising role of leveraging PBPK models to extrapolate discoveries from IVIVE toxicity studies to assess nanomaterial safety in humans.

Future directions for nanomaterial PBPK modelling approaches

In the context of simulating nanomaterial disposition and pharmacokinetic profiles with PBPK-based methodologies, three challenges remain outstanding. The first challenge is how best to represent nanomaterial metabolism and related chemical degradation processes into model designs, equations, and parameters. Species variations in liver enzyme function (e.g., microsomal P450 systems) can lead to remarkably differences in the pharmacodynamics and toxicities of metabolised drugs [102, 103]. Most of the nanomaterial PBPK models reported in literature circumvent this issue because the nanomaterial types studied—predominantly inorganic and polymeric—are practically nondegradable on the timescale of most physiological processes. However, chemical and metabolic transformations in the context of even nondegradable nanomaterials can lead to significant changes in their physicochemical properties and organ distributions. For example, degradation of the polymeric shell coating PEGylated gold nanoparticles by proteolytic enzymes in the liver transformed the properties and integrity of the nanoparticles, producing divergent distribution patterns between the gold core (to the liver) and the polymer fragments (to the kidneys) [104]. Similar property changes to nanomaterials may lead to aggregation or agglomeration in tissues or in endocytic cells[57], affecting their biophysicochemical interactions and ultimately their disposition profiles in a manner undescribed with conventional PBPK model equations and physiological parameters [90, 105, 106]. An obstacle to better understandings of nanomaterial aggregation and degradation is the lack of reliable analytical techniques for directly measuring and characterising these transformations in vivo. Consequently, first-order time-dependent degradation kinetics are commonly assumed for most nanomaterials [90, 106]. In vitro assays can play a significant role by estimating the degradation rate constants as initial values of model parameters, which can be further optimised by fitting the model with available experimental data.

Another challenge yet to be addressed is how to account for the transportation kinetics of lymphatic uptake. Few examples of PBPK frameworks representing the lymphatic system uptake of intravenous nanomaterials are available, in spite of it's known role for accumulating macromolecule drugs and nanomaterials from the tissue interstitium and altering their overall disposition [106, 107]. The challenge with representing the lymphatics is the additional complexity and uncertainty they add to PBPK model structures and mathematical descriptions of the convectional (or cyclical) transportation of nanomaterials between the lymphatic system and tissue interstitial space, and the blood circulation via deposition (as in Figure 5C). Therefore, without sufficiently detailed experimental data on nanomaterial disposition in the lymph, the validation of model assumptions regarding lymphatic structures and transportation parameters is very difficult. It has been suggested that for most intravenously administered nanomaterials, since the MPS organ uptake will usually dominate lymphatic accumulation, the omission of lymphatic uptake is a reasonable compromise to avoid unsolvable PBPK models [90]. However, this assumption requires careful consideration of nanomaterial types that share physicochemical properties notable for specific enhancement of nanomaterial accumulation in lymph nodes [107].

Finally, representations of tumours in PBPK models of nanomaterials remain largely unexplored, despite the extensive uses of nanomaterials for preclinical and clinical applications in tumour theranostics and drug delivery. Owing to their abnormal physiological features and highly variable transportation mechanisms, modelling the kinetics of nanomaterial deposition in tumour tissue can be especially challenging[108]. The dominant transportation phenomena in tumours for intravenously nanomaterials is the EPR effect, wherein the leaky tumour vasculature permits the preferential extravasation of long circulating nanomaterials into the tumour interstitium [109]. The extent of this accumulation can vary depending on the characteristics of the nanomaterial (e.g., size and shape), the heterogeneity of blood flow and microvascular permeability, structural barriers, intratumoural pressure, and reduced lymphatic drainage [109]. Unsurprisingly, there have been well documented and significant differences in the EPR effect and nanomaterial delivery among different tumour types (e.g., breast, lung, colon, etc.) and between animal tumour models and similar tumours in patients [110].

PBPK-based modelling efforts for nanomaterial tumour uptake have traditionally focused on simulating anticancer drug release kinetics into the tumour interstitium or tumour cells. The approaches described so far have ranged in complexity from simple single tumour compartment representations [111, 112] to intricate tumour structures subdivided into vascular, interstitial, and cellular sub-compartments (Figure 6A) [81, 113]. The advantages of complex PBPK tumour models are the mechanistic insights they can provide regarding the distribution of nanomaterials in tumours and their overall therapeutic efficacy. However, practical disadvantages with model complexity include: (i) lack of data from literature to estimate initial model parameters and (ii) the necessity for obtaining highly detailed experimental data of nanomaterial tumour disposition in order to appropriately validate model parameters and assumptions. As a compromise on complexity, it has been suggested that the two-pore compartment formalism might be leveraged for modelling tumour uptake of nanomaterial since it can account for kinetic transport differences such as passive diffusion of nanomaterials from blood vessels into tumours versus convective-based EPR effects (Figure 6B) [106]. Experimental evidence has demonstrated that nanomaterial tumour permeability is at least partially dependent upon vascular pore size, but the sizes of pores in animal xenograft can be highly variable, ranging from hundreds of nanometres to microns [114, 115]. Examples of the two-pore compartment approach for PBPK-based modelling of nanomaterial disposition in tumours have yet to be reported.

 Figure 6 

Representations of tumour compartments in nanomaterial PBPK models. A. Complex representation of a multi-compartmental tumour structure subdivided into vascular, interstitial, and cellular sub-compartments and using the membrane limited organ model. The solid lines represent the transport of the nanomaterial and the dashed lines the transport of the payload. Graphic adapted from [121]. B. Generic representation of tumour using the two-pore compartment formalism. The large pores (1.5 μm here) model transport of nanomaterials through intercellular openings due to convection (i.e., EPR effect) and the small pores (0.6 μm here) passive diffusion into and out of the tumour via transcellular pores [115]. Note that the mathematical description of transport kinetics (as opposed to physical pore size) are what matters for model design work. These models generally yield superior simulations compared to standard membrane limited (or one-pore) models for antibodies [119]. Graphic adapted from [118].

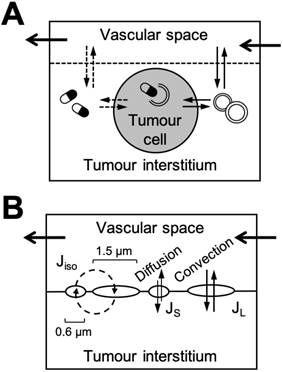
Summary of PBPK modelling of nanomaterial disposition and pharmacokinetic profiles

The development and application of mechanistic PBPK modelling for nanomaterial biokinetics has been steadily growing over the past decade, with useful demonstrations for the rational design of nanomaterial properties and for extrapolating nanomaterial dispositions profiles in humans for toxicity assessments. The advantage of this extrapolation approach is that the scaling of pharmacokinetic profiles between species is based on physiological (system) information (as opposed to assumptions of interspecies scaling relationships) that can better represent the key physiological and biological determinants of nanomaterial disposition. Thus, PBPK models can be powerful quantitative tool for understanding and predicting dose-response relationships and toxicity hazards of nanomaterials in untested species during the discovery and development phases. However, challenges still remain over how best to represent in a PBPK framework (i.e., with rate equations and model parameters), the complex transport mechanisms underlying nanomaterial disposition such as passive diffusion, MPS uptake, the EPR effect, etc. For now, the oversimplification of these nanomaterial and species dependent phenomena to a single mechanism may be advantageous for ensuring PBPK models do not become too complex to solve. Future modelling efforts for nanomaterials will require more comprehensive study of these physiological mechanisms individually, especially if these are found to result in disposition profiles resulting in toxicities. The best strategies for applying PBPK modelling embrace iterative modification to the model designs, equations, parameters and assumptions upon the availability of new preclinical knowledge and clinical observations (so-called “predict-learn-confirm” cycles) in order to create a more accurate tool for stimulating nanomaterial disposition and pharmacokinetics in humans.

Overall, the following points can be concluded for PBPK modelling tools of nanomaterial disposition and pharmacokinetics in humans:

• Whole body PBPK models designed for simulating nanomaterial disposition and pharmacokinetic profiles, and optimised with preclinical rodent and nonrodent data, have successfully simulated distribution profiles observed in humans. Most PBPK models are currently designed and optimised for a single nanomaterial type, although efforts to create generalisable models based on quantitative nanomaterial property-ADME profile relationships are ongoing.
• Nanomaterial property-related model parameters such as the distribution coefficient and parameters describing the MPS uptake and endocytosis can be estimated reasonably from data-fitting with acceptable sensitivity coefficients. However, attention should be paid to the physiological differences between preclinical animals and humans, particularly with respects to species-specific differences in the MPS and primary elimination organs (see Box 1), overlooking of which can lead to inaccurate stimulated data in humans.
• Representation of the MPS uptake of nanomaterials as membrane rate limited endocytosis sub-compartments is a required design feature in many nanomaterial PBPK models. Selection of the appropriate representation for MPS uptake and endocytosis will depend on the nanomaterial types and their physicochemical characteristics, and the availability of experimental data (preferably from IVIVE studies) with which to validate PBPK model parameters and assumptions.
• PBPK models can be used to generate insightful hypotheses for nanomaterial toxicokinetic and toxicologic profiles in humans, and for extrapolating from test species the MRSD for clinical phase 1 trials. Predicting toxicities and adverse events in humans with PBPK modelling remains limited since the mechanisms of toxicities on the scale of an entire living organism are often complex and unanticipated. Irritative modification of nanomaterial-based PBPK models with updated preclinical and clinical observations of disposition and toxicity will improve their predictiveness for untested clinical outcomes in humans.
• Challenges remain regarding the appropriate representations in PBPK frameworks for nanomaterial metabolism and related chemical degradation processes, and for the uptake and transportation of nanomaterials in the lymphatic system and tumours. Addressing these challenges will require balancing model complexity with the availability of experimental with which to validate model parameters.

Box 2. The design of physiologically based pharmacokinetic (PBPK) models for nanomaterials.

The first step in the design of every PBPK model is the selection of appropriate organs and tissues to represent in the structure. Core tissues typically include the blood compartments, the eliminating organs, sites of administration (i.e., if not intravenous) or sites of action, and any other organ expected to contribute significantly to the mass balance of the nanomaterial. The organs are arranged anatomically and with attention to blood flow patterns, as in the hepatic portal system, and clearance pathways (as in Figure 4B). A practical consideration when selecting organs to represent in a model structure is the availability of experimental data and information on tissue-specific nanomaterial interactions. Overly complex models create challenges and uncertainties for parameter estimation and model validation. When metabolic products are also of interest, a parallel sub-PBPK structure can be created for each metabolite originating at the site of biotransformation and transiting to all the other compartments in the model.

The second step is to describe the movement of nanomaterials within each organ compartment with a mass balance differential equation. All the compartments of a PBPK model are interconnected through the time-dependent mass transportation of the nanomaterial and its metabolite(s) passing among them through blood circulation. The mass transfer functions governing each organ can be considered either perfusion rate limited or permeability rate (or membrane) limited. Perfusion rate limited organs assume that nanomaterial transport into and distribution throughout the organ is instantaneous and without the creation of concentration gradients within (i.e., a well-stirred compartment assumption). In these organs, the rate-limiting step controlling to movement of nanomaterials into and out of the organ is the blood flow to the organ. Perfusion rate limited PBPK models have been used to study quantum dots [98, 116]. However, subsequent studies revealed that this compartment assumption could not adequately predict the complex tissue pharmacokinetics quantum dot nanomaterials exhibited in the liver and kidneys [98, 117].

Conversely, membrane limited organs integrate membrane barriers that restrict the distribution of nanomaterials within the organ, typically by creating one or more well-stirred sub-compartments with permeability rate limited transfer between each (as in Figure 5A-B). Practically, the use of membrane limited organ model should be adopted if the tissue-nanomaterial concentration does not decline in parallel with concentration in the blood. Numerous reports of PBPK-based nanomaterial modelling have determined that simulations with membrane limited organ models yield superior correlation coefficients with experimental data in comparison to perfusion rate limited models, especially for smaller sized and strongly charged nanomaterials [95, 99].

A third variation of the membrane limited model is known as the two-pore formalism, intended for explaining the paracellular transport of antibodies (~145 kDa) and other macromolecules into the interstitial space through differently sized pores in blood vessel walls (as in Figure 6B) [118, 119]. This model was developed to account for the unique biphasic relationship between molecular weight and membrane permeability exhibited by macromolecules crossing capillary walls in vivo. It was proposed that two set of pathways exist for paracellular transportation: a system of small (~45 Å) pores for passive diffusion and a system of large (~250 Å) pore for convective-based passage. Although this model requires complex mathematical representations for the different osmotic reflections and flow rates between each pore size, the resulting simulations are generally superior to standard membrane limited (or one-pore) models [119]. The two-pore model is of particular interest for nanomaterial modelling since convective transport-based effects such as the EPR effect are regarded as the dominant transportation mechanism for accumulation in tumours [106].

The third step is to create and define model parameters, including physiological constants and nanomaterial-specific factors that together describe mathematically the nanomaterial's disposition. Physiological parameters (e.g., blood flows, tissue volumes, tissue composition, etc.) are nanomaterial independent and can usually be retrieved from literature. On the other hand, physicochemical- and biochemical-related model parameters (e.g., tissue-to-plasma distribution coefficient, tissue permeability-surface area product, enzymatic activity, etc.) are nanomaterial dependent and must be determined either by estimation from data-fitting or empirically from in vitro to in vivo extrapolation studies. The typical approach for parameter estimation begins with setting the physiological parameters to a value defined in literature, followed by irritative simulation of the nanomaterial-specific parameters and fitting against experimental data until strong correlations between the simulated and measured data are obtained.

A nanomaterial-specific parameter of particular interest for modelling nanomaterials is the tissue-to-plasma distribution (or partition) coefficient, a parameter that accounts for the uneven steady state distribution of nanomaterials between the interstitial tissue fluid and the blood plasma in each organ. This model parameter is estimated empirically and represents the influence of several physiological processes such as disposition (ADME), protein binding (protein corona formation) or opsonization, transportation through blood capillaries, phagocytosis, transcytosis, and endocytosis. For nanomaterials, the distribution coefficient favours higher concentrations in the vascular compartment over the tissue (interstitial) space; it has been suggested that differences in the composition of the protein corona between the blood and interstitial environments greatly shapes nanomaterial interactions with blood vessel mural cells [63, 94, 105]. Regardless of its physiological interpretation, the practical purpose of the distribution coefficient is to improve the correlation of PBPK model simulations with experimental data, and there is growing evidence for the early-phase pharmacokinetics of smaller sized nanomaterials this parameter is especially significant [97, 120].

The final step of PBPK model development is to estimate and optimise the nanomaterial-dependent model parameters using experimental data and a numerical integration algorithm (e.g., fourth-order Runge-Kutta method, Markov chain Monte Carlo (MCMC) techniques, etc.) to solve the set of mass balance (ordinary) differential equations [31]. Because available PBPK modelling software has limited functionalities for nanomaterials, investigators typically must program their models into numerical analysis software (e.g., MATLAB-Simulink, ACSL/acslXtreme, etc.) and solve the differential equations to obtain the optimised parameters. With optimised parameters estimated, the model is lastly validated against an independent dataset to confirm the model assumptions and parameter values. Validation also includes a parameter sensitivity analysis and an uncertainty analysis to identify highly influential parameters whose impact on the simulation is greatest. Notably, both nanomaterial-dependent and physiological (or nanomaterial-independent) parameters can be identified upon sensitivity analysis as being impactful on the simulation.

Conclusion

The investigators toolbox for interpreting and extrapolating disposition (ADME), pharmacokinetic and toxicokinetic data of nanomaterials in multiple species continues to expand as better modelling approaches and more experimental data are continually being added. Unfortunately, the challenges and nuances of studying nanomaterial disposition and pharmacokinetics is widely underappreciated and oftentimes misapplied. Herein we have highlighted two complementary research tools for assisting investigators with understanding the principles of interspecies extrapolation and modelling approaches (Figure 1), current applications, and the advantages and limitations of each. Allometric scaling relationships are routinely used (and expected by regulatory agencies) to extrapolate nanomaterial pharmacokinetics in humans and to establish the MRSD for clinical phase 1 trials in spite of acknowledged limitations with this extrapolation approach's accounting for the exceptional properties and in vivo behaviours of nanomaterials. Mechanistic PBPK models for simulating nanomaterial disposition and pharmacokinetic profiles are steadily improving in sophistication (e.g., for representing nanomaterial transport phenomena), and evidence for their use in de novo analyses of investigational and clinically-approved nanomaterials is growing. With proper knowledge and consideration of the challenges and requirements for using these research tools, the clinical translation and development of promising nanomaterial candidates will undoubtedly benefit from more accurate predictions of pharmacokinetic parameters and dose, and assessments of safety and toxicity in humans.

Abbreviations

ADME: absorption, distribution, metabolism, and elimination; AUC: area under the curve; BMR: basal metabolic rate; CARPA: complement activation-related pseudo-allergy; CL: (systemic) clearance; EPR: enhanced permeability and retention (effect); GFR: glomerular filtration rate; HED: human equivalent dose; IVIVE: in vitro in vivo extrapolation (studies); MABEL: minimum anticipated biological effect level; MCMC: Markov chain Monte Carlo (statistics); MLP: maximum life-span potential; mPEG: methoxypolyethylene glycol; MPS: mononuclear phagocyte system; MRSD: maximum recommended starting dose; MTD: maximum tolerated dose; MW: molecular weight; NOAEL: no-observed adverse effect level; PAMAM: poly(amidoamine); PBPK: physiologically based pharmacokinetic (modelling); PEG: polyethylene glycol; PLGA: poly(lactic-co-glycolic acid); PSMA: prostate specific membrane antigen; ROE: (Mahmood's) rule of exponents; ROS: radical oxygen species; siRNA: small interfering ribonucleic acid; USFDA: United States Food and Drug Administration; WBPBPK: whole body physiologically based pharmacokinetic (modelling).

Acknowledgements

The authors are supported by the Terry Fox Research Institute, the Canadian Institute of Health Research, the Natural Sciences and Engineering Research Council of Canada, and the Princess Margaret Cancer Foundation.

Competing Interests

The authors have declared that no competing interest exists.

References

1. Woodle MC, Lasic DD. Sterically stabilized liposomes. Biochim Biophys Acta - Rev Biomembr. 1992;1113:171-199

2. Papahadjopoulos D, Allen TM, Gabizon A, Mayhew E, Matthay K, Huang SK. et al. Sterically stabilized liposomes: improvements in pharmacokinetics and antitumor therapeutic efficacy. Proc Natl Acad Sci U S A. 1991;88:11460-4

3. Hu C-MJ, Fang RH, Aryal S, Cheung C, Zhang L. Erythrocyte membrane-camouflaged polymeric nanoparticles as a biomimetic delivery platform. Proc Natl Acad Sci. 2011;108:10980-10985

4. Parodi A, Quattrocchi N, Van De Ven AL, Chiappini C, Evangelopoulos M, Martinez JO. et al. Synthetic nanoparticles functionalized with biomimetic leukocyte membranes possess cell-like functions. Nat Nanotechnol. 2013;8:61-68

5. Tsai RK, Rodriguez PL, Discher DE, Pantano DA, Harada T, Christian DA. Minimal “self” peptides that inhibit phagocytic clearance and enhance delivery of nanoparticles. Science. 2013;339:971-975

6. Liu T, Choi H, Zhou R, Chen I-W. RES blockade: a strategy for boosting efficiency of nanoparticle drug. Nano Today. 2015;10:11-21

7. Tavares AJ, Poon W, Zhang Y-N, Dai Q, Besla R, Ding D. et al. Effect of removing kupffer cells on nanoparticle tumor delivery. Proc Natl Acad Sci. 2017;114:E10871-E10880

8. Zamboni WC, Szebeni J, Kozlov S V, Lucas AT, Piscitelli JA, Dobrovolskaia MA. Animal models for analysis of immunological responses to nanomaterials: challenges and considerations. Adv Drug Deliv Rev. 2018;136-137:82-96

9. Parhiz H, Khoshnejad M, Myerson JW, Hood E, Patel PN, Brenner JS. et al. Unintended effects of drug carriers: big issues of small particles. Adv Drug Deliv Rev. 2018;130:90-112

10. Caron WP, Clewell H, Dedrick R, Ramanathan RK, Davis WL, Yu N. et al. Allometric scaling of pegylated liposomal anticancer drugs. J Pharmacokinet Pharmacodyn. 2011;38:653-669

11. Caron WP, Morgan KP, Zamboni BA, Zamboni WC. A review of study designs and outcomes of phase i clinical studies of nanoparticle agents compared with small-molecule anticancer agents. Clin Cancer Res. 2013;19:3309-3315

12. Davidson IWF, Parker JC, Beliles RP. Biological basis for extrapolation across mammalian species. Regul Toxicol Pharmacol. 1986;6:211-237

13. Boxenbaum H, DiLea C. First-time-in-human dose selection: allometric thoughts and perspectives. J Clin Pharmacol. 1995;35:957-966

14. Mahmood I, Green MD, Fisher JE. Selection of the first-time dose in humans: comparison of different approaches based on interspecies scaling of clearance. J Clin Pharmacol. 2003;43:692-7

15. Fuse E, Kobayashi T, Inaba M, Sugiyama Y. Prediction of the maximal tolerated dose (MTD) and therapeutic effect of anticancer drugs in humans: integration of pharmacokinetics with pharmacodynamics and toxicodynamics. Cancer Treat Rev. 1995;21:133-157

16. Hu T-M, Hayton WL. Allometric scaling of xenobiotic clearance: uncertainty versus universality. AAPS PharmSci. 2001;3:30-43

17. Huh Y, Smith DE, Rose Feng M. Interspecies scaling and prediction of human clearance: comparison of small- and macro-molecule drugs. Xenobiotica. 2011;41:972-987

18. Heusner AA. Energy metabolism and body size I. Is the 0.75 mass exponent of Kleiber's equation a statistical artifact?. Respir Physiol. 1982;48:1-12

19. Lee SJ, Koo H, Jeong H, Huh MS, Choi Y, Jeong SY. et al. Comparative study of photosensitizer loaded and conjugated glycol chitosan nanoparticles for cancer therapy. J Control Release. 2011;152:21-29

20. Feldman HA, McMahon TA. The mass exponent for energy metabolism is not a statistical artifact. Respir Physiol. 1983;52:149-163

21. Mahmood I. Theoretical versus empirical allometry: facts behind theories application to pharmacokinetics. J Pharm Sci. 2010;99:2927-2933

22. Mahmood I. Role of fixed coefficients and exponents in the prediction of human drug clearance: how accurate are the predictions from one or two species?. J Pharm Sci. 2009;98:2472-2493

23. Tang H, Hussain A, Leal M, Fluhler E, Mayersohn M. Controversy in the allometric application of fixed- versus varying-exponent models: a statistical and mathematical perspective. J Pharm Sci. 2011;100:402-410

24. Moghimi SM, Hunter AC, Andresen TL. Factors controlling nanoparticle pharmacokinetics: an integrated analysis and perspective. Annu Rev Pharmacol Toxicol. 2012;52:481-503

25. Kang H, Mintri S, Menon AV, Lee HY, Choi HS, Kim J. Pharmacokinetics, pharmacodynamics and toxicology of theranostic nanoparticles. Nanoscale. 2015;7:18848-18862

26. Aillon KL, Xie Y, El-Gendy N, Berkland CJ, Forrest ML. Effects of nanomaterial physicochemical properties on in vivo toxicity. Adv Drug Deliv Rev. 2009;61:457-466

27. Wajima T, Fukumura K, Yano Y, Oguma T. Prediction of human pharmacokinetics from animal data and molecular structural parameters using multivariate regression analysis: oral clearance. J Pharm Sci. 2003;92:2427-2440

28. Nagilla R, Ward KW. A comprehensive analysis of the role of correction factors in the allometric predictivity of clearance from rat, dog, and monkey to humans. J Pharm Sci. 2004;93:2522-2534

29. Lucas AT, Herity LB, Kornblum ZA, Madden AJ, Gabizon A, Kabanov A V. et al. Pharmacokinetic and screening studies of the interaction between mononuclear phagocyte system and nanoparticle formulations and colloid forming drugs. Int J Pharm. 2017;526:443-454

30. Sharma V, McNeill JH. To scale or not to scale: the principles of dose extrapolation. Br J Pharmacol. 2009;157:907-921

31. Espié P, Tytgat D, Sargentini-Maier M-L, Poggesi I, Watelet J-B. Physiologically based pharmacokinetics (PBPK). Drug Metab Rev. 2009;41:391-407

32. Lavé T, Coassolo P, Reigner B. Prediction of hepatic metabolic clearance based on interspecies allometric scaling techniques and in vitro-in vivo correlations. Clin Pharmacokinet. 1999;36:211-231

33. Huang Q, Riviere JE. The application of allometric scaling principles to predict pharmacokinetic parameters across species. Expert Opin Drug Metab Toxicol. 2014;10:1241-1253

34. Mahmood I. Interspecies scaling: role of protein binding in the prediction of clearance from animals to humans. J Clin Pharmacol. 2000;40:1439-46

35. Mahmood I, Balian JD. Interspecies scaling: predicting clearance of drugs in humans. Three different approaches. Xenobiotica. 1996;26:887-895

36. Mahmood I. Interspecies scaling of protein drugs: prediction of clearance from animals to humans. J Pharm Sci. 2004;93:177-185

37. Mahmood I, Balian JD. Interspecies scaling: predicting pharmacokinetic parameters of antiepileptic drugs in humans from animals with special emphasis on clearance. J Pharm Sci. 1996;85:411-414

38. Stern ST, Hall JB, Yu LL, Wood LJ, Paciotti GF, Tamarkin L. et al. Translational considerations for cancer nanomedicine. J Control Release. 2010;146:164-174

39. Dedrick R, Bischoff KB, Zaharko DS. Interspecies correlation of plasma concentration history of methotrexate (NSC-740). Cancer Chemother Rep. 1970;54:95-101

40. Boxenbaum H, Ronfeld R. Interspecies pharmacokinetic scaling and the Dedrick plots. Am J Physiol Integr Comp Physiol. 1983;245:R768-R775

41. Mahmood I. Interspecies scaling: predicting volumes, mean residence time and elimination half-life.* Some suggestions. J Pharm Pharmacol. 1998;50:493-499

42. Lv W, Guo J, Ping Q, Song Y, Li J. Comparative pharmacokinetics of breviscapine liposomes in dogs, rabbits and rats. Int J Pharm. 2008;359:118-122

43. Hrkach J, Von Hoff D, Ali MM, Andrianova E, Auer J, Campbell T. et al. Preclinical development and clinical translation of a PSMA-targeted docetaxel nanoparticle with a differentiated pharmacological profile. Sci Transl Med. 2012;4:128ra39-128ra39

44. Eliasof S, Lazarus D, Peters CG, Case RI, Cole RO, Hwang J. et al. Correlating preclinical animal studies and human clinical trials of a multifunctional, polymeric nanoparticle. Proc Natl Acad Sci. 2013;110:15127-15132

45. Gabizon A, Catane R, Uziely B, Kaufman B, Safra T, Cohen R. et al. Prolonged circulation time and enhanced accumulation in malignant exudates of doxorubicin encapsulated in polyethylene-glycol coated liposomes. Cancer Res. 1994;54:987-92

46. Zamboni WC, Strychor S, Joseph E, Walsh DR, Zamboni BA, Parise RA. et al. Plasma, tumor, and tissue disposition of STEALTH liposomal CKD-602 (S-CKD602) and nonliposomal CKD-602 in mice bearing A375 human melanoma xenografts. Clin Cancer Res. 2007;13:7217-7223

47. Tsoi KM, MacParland SA, Ma X-Z, Spetzler VN, Echeverri J, Ouyang B. et al. Mechanism of hard-nanomaterial clearance by the liver. Nat Mater. 2016;1:1-10

48. Zhang Y-N, Poon W, Tavares AJ, McGilvray ID, Chan WCW. Nanoparticle-liver interactions: cellular uptake and hepatobiliary elimination. J Control Release. 2016;240:332-348

49. Caron WP, Lay JC, Fong AM, La-Beck NM, Kumar P, Newman SE. et al. Translational studies of phenotypic probes for the mononuclear phagocyte system and liposomal pharmacology. J Pharmacol Exp Ther. 2013;347:599-606

50. Paciotti GF, Myer L, Weinreich D, Goia D, Pavel N, McLaughlin RE. et al. Colloidal gold: a novel nanoparticle vector for tumor directed drug delivery. Drug Deliv. 2004;11:169-183

51. Libutti SK, Paciotti GF, Byrnes AA, Alexander HR, Gannon WE, Walker M. et al. Phase I and pharmacokinetic studies of CYT-6091, a novel pegylated colloidal gold-rhtnf nanomedicine. Clin Cancer Res. 2010;16:6139-6149

52. De Jong WH, Hagens WI, Krystek P, Burger MC, Sips AJAM, Geertsma RE. Particle size-dependent organ distribution of gold nanoparticles after intravenous administration. Biomaterials. 2008;29:1912-1919

53. Von Hoff DD, Mita MM, Ramanathan RK, Weiss GJ, Mita AC, LoRusso PM. et al. Phase I study of PSMA-targeted docetaxel-containing nanoparticle BIND-014 in patients with advanced solid tumors. Clin Cancer Res. 2016;22:3157-3163

54. Weiss GJ, Chao J, Neidhart JD, Ramanathan RK, Bassett D, Neidhart JA. et al. First-in-human phase 1/2a trial of CRLX101, a cyclodextrin-containing polymer-camptothecin nanopharmaceutical in patients with advanced solid tumor malignancies. Invest New Drugs. 2013;31:986-1000

55. Schluep T, Cheng J, Khin KT, Davis ME. Pharmacokinetics and biodistribution of the camptothecin-polymer conjugate IT-101 in rats and tumor-bearing mice. Cancer Chemother Pharmacol. 2006;57:654-662

56. Schluep T, Hwang J, Hildebrandt IJ, Czernin J, Choi CHJ, Alabi CA. et al. Pharmacokinetics and tumor dynamics of the nanoparticle IT-101 from PET imaging and tumor histological measurements. Proc Natl Acad Sci. 2009;106:11394-11399

57. Zuckerman JE, Gritli I, Tolcher A, Heidel JD, Lim D, Morgan R. et al. Correlating animal and human phase Ia/Ib clinical data with CALAA-01, a targeted, polymer-based nanoparticle containing siRNA. Proc Natl Acad Sci. 2014;111:11449-11454

58. Zuckerman JE, Choi CHJ, Han H, Davis ME. Polycation-siRNA nanoparticles can disassemble at the kidney glomerular basement membrane. Proc Natl Acad Sci. 2012;109:3137-3142

59. Heidel JD, Yu Z, Liu JY-C, Rele SM, Liang Y, Zeidan RK. et al. Administration in non-human primates of escalating intravenous doses of targeted nanoparticles containing ribonucleotide reductase subunit M2 siRNA. Proc Natl Acad Sci. 2007;104:5715-5721

60. Tenzer S, Docter D, Rosfa S, Wlodarski A, Kuharev J, Rekik A. et al. Nanoparticle size is a critical physicochemical determinant of the human blood plasma corona: A comprehensive quantitative proteomic analysis. ACS Nano. 2011;5:7155-7167

61. Tenzer S, Docter D, Kuharev J, Musyanovych A, Fetz V, Hecht R. et al. Rapid formation of plasma protein corona critically affects nanoparticle pathophysiology. Nat Nanotechnol. 2013;8:772-781

62. Darabi Sahneh F, Scoglio C, Riviere J. Dynamics of nanoparticle-protein corona complex formation: analytical results from population balance equations. PLoS One. 2013;8:e64690

63. Sahneh FD, Scoglio CM, Monteiro-Riviere NA, Riviere JE. Predicting the impact of biocorona formation kinetics on interspecies extrapolations of nanoparticle biodistribution modeling. Nanomedicine. 2015;10:25-33

64. Bertrand N, Grenier P, Mahmoudi M, Lima EM, Appel EA, Dormont F. et al. Mechanistic understanding of in vivo protein corona formation on polymeric nanoparticles and impact on pharmacokinetics. Nat Commun. 2017;8:777

65. Riviere JE. Of mice, men and nanoparticle biocoronas: are in vitro to in vivo correlations and interspecies extrapolations realistic?. Nanomedicine. 2013;8:1357-1359

66. Caracciolo G, Pozzi D, Capriotti AL, Cavaliere C, Piovesana S, La Barbera G. et al. The liposome-protein corona in mice and humans and its implications for in vivo delivery. J Mater Chem B. 2014;2:7419-7428

67. Pozzi D, Caracciolo G, Capriotti AL, Cavaliere C, La Barbera G, Anchordoquy TJ. et al. Surface chemistry and serum type both determine the nanoparticle-protein corona. J Proteomics. 2015;119:209-217

68. Gibson CR, Sandhu P, Hanley WD. Monoclonal antibody pharmacokinetics and pharmacodynamics. eds. Hoboken, NJ, USA, John Wiley & Sons, Inc. 2009:439-460

69. Szebeni J, Simberg D, González-Fernández Á, Barenholz Y, Dobrovolskaia MA. Roadmap and strategy for overcoming infusion reactions to nanomedicines. Nat Nanotechnol. 2018;13:1100-1108

70. Voisin EM, Ruthsatz M, Collins JM, Hoyle PC. Extrapolation of animal toxicity to humans: Interspecies comparisons in drug development. Regul Toxicol Pharmacol. 1990;12:107-116

71. Reigner BG, Blesch K. Estimating the starting dose for entry into humans: principles and practice. Eur J Clin Pharmacol. 2002;57:835-845

72. Imam MT, Venkateshan SP, Tandon M, Saha N, Pillai KK. Comparative evaluation of US Food and Drug Administration and pharmacologically guided approaches to determine the maximum recommended starting dose for first-in-human clinical trials in adult healthy men. J Clin Pharmacol. 2011;51:1655-1664

73. Hyafil F, Cornily J-C, Feig JE, Gordon R, Vucic E, Amirbekian V. et al. Noninvasive detection of macrophages using a nanoparticulate contrast agent for computed tomography. Nat Med. 2007;13:636-641

74. Moghimi SM, Hunter C. Capture of stealth nanoparticles by the body's defences. Crit Rev Ther Drug Carr Syst. 2001;18:24

75. Cesta MF. Normal structure, function, and histology of the spleen. Toxicol Pathol. 2006;34:455-465

76. Demoy M, Andreux JP, Weingarten C, Gouritin B, Guilloux V, Couvreur P. Spleen capture of nanoparticles: influence of animal species and surface characteristics. Pharm Res. 1999;16:37-41

77. Bronte V, Pittet MJ. The spleen in local and systemic regulation of immunity. Immunity. 2013;39:806-818

78. Moghimi SM, Hedeman H, Muir IS, Illum L, Davis SS. An investigation of the filtration capacity and the fate of large filtered sterically-stabilized microspheres in rat spleen. Biochim Biophys Acta - Gen Subj. 1993;1157:233-240

79. Moghimi S. Chemical camouflage of nanospheres with a poorly reactive surface: towards development of stealth and target-specific nanocarriers. Biochim Biophys Acta - Mol Cell Res. 2002;1590:131-139

80. Braet F, Wisse E, F B, E W. Structural and functional aspects of liver sinusoidal endothelial cell fenestrae: a review. Comp Hepatol. 2002;1:1

81. Harashima H, Komatsu S, Kojima S, Yanagi C, Morioka Y, Naito M. et al. Species difference in the disposition of liposomes among mice, rats, and rabbits: allometric relationship and species dependent hepatic uptake mechanism. Pharm Res. 1996;13:1049-1054

82. Liu D, Hu Q, Song YK. Liposome clearance from blood: different animal species have different mechanisms. Biochim Biophys Acta - Biomembr. 1995;1240:277-284

83. Hussain MM, Mahley RW, Boyles JK, Lindquist PA, Brecht WJ, Innerarity TL. et al. Chylomicron metabolism. Chylomicron uptake by bone marrow in different animal species. J Biol Chem. 1989;264:17931-17938

84. Winkler GC. Pulmonary intravascular macrophages in domestic animal species: Review of structural and functional properties. Am J Anat. 1988;181:217-234

85. Brain JD, Molina RM, DeCamp MM, Warner AE. Pulmonary intravascular macrophages: their contribution to the mononuclear phagocyte system in 13 species. Am J Physiol Cell Mol Physiol. 1999;276:L146-L154

86. Csukás D, Urbanics R, Wéber G, Rosivall L, Szebeni J. Pulmonary intravascular macrophages: prime suspects as cellular mediators of porcine CARPA. Eur J Nanomedicine. 2015;7:27-36

87. Schneberger D, Aharonson-Raz K, Singh B. Pulmonary intravascular macrophages and lung health: what are we missing?. Am J Physiol Cell Mol Physiol. 2012;302:L498-L503

88. Lin JH. Species similarities and differences in pharmacokinetics. Drug Metab Dispos. 1995;23:1008-21

89. Xu J, Yu M, Peng C, Carter P, Tian J, Ning X. et al. Dose dependencies and biocompatibility of renal clearable gold nanoparticles: from mice to non-human primates. Angew Chemie Int Ed. 2018;57:266-271

90. Li M, Al-Jamal KT, Kostarelos K, Reineke J. Physiologically based pharmacokinetic modeling of nanoparticles. ACS Nano. 2010;4:6303-6317

91. Storm G, Belliot SO, Daemen T, Lasic DD. Surface modification of nanoparticles to oppose uptake by the mononuclear phagocyte system. Adv Drug Deliv Rev. 1995;17:31-48

92. Owens III D, Peppas N. Opsonization, biodistribution, and pharmacokinetics of polymeric nanoparticles. Int J Pharm. 2006;307:93-102

93. Kagan L, Gershkovich P, Wasan KM, Mager DE. Dual physiologically based pharmacokinetic model of liposomal and nonliposomal amphotericin b disposition. Pharm Res. 2014;31:35-45

94. Li D, Johanson G, Emond C, Carlander U, Philbert M, Jolliet O. Physiologically based pharmacokinetic modeling of polyethylene glycol-coated polyacrylamide nanoparticles in rats. Nanotoxicology. 2014;8:128-137

95. Lin Z, Monteiro-Riviere NA, Riviere JE. A physiologically based pharmacokinetic model for polyethylene glycol-coated gold nanoparticles of different sizes in adult mice. Nanotoxicology. 2015;10:1-11

96. Lin Z, Monteiro-Riviere NA, Kannan R, Riviere JE. A computational framework for interspecies pharmacokinetics, exposure and toxicity assessment of gold nanoparticles. Nanomedicine. 2016;11:107-119

97. Carlander U, Li D, Jolliet O, Emond C, Johanson G. Toward a general physiologically-based pharmacokinetic model for intravenously injected nanoparticles. Int J Nanomedicine. 2016;11:625

98. Lee HA, Leavens TL, Mason SE, Monteiro-Riviere NA, Riviere JE. Comparison of quantum dot biodistribution with a blood-flow-limited physiologically based pharmacokinetic model. Nano Lett. 2009;9:794-799

99. Reineke J, Li M, Avgoustakis K. Physiologically based pharmacokinetic modeling of PLGA nanoparticles with varied mPEG content. Int J Nanomedicine. 2012;7:1345

100. Mager DE, Mody V, Xu C, Forrest A, Lesniak WG, Nigavekar SS. et al. Physiologically based pharmacokinetic model for composite nanodevices: effect of charge and size on in vivo disposition. Pharm Res. 2012;29:2534-2542

101. McSweeney MD, Wessler T, Price LSL, Ciociola EC, Herity LB, Piscitelli JA. et al. A minimal physiologically based pharmacokinetic model that predicts anti-PEG IgG-mediated clearance of PEGylated drugs in human and mouse. J Control Release. 2018;284:171-178

102. Shimada T, Mimura M, Inoue K, Nakamura S, Oda H, Ohmori S. et al. Cytochrome P450-dependent drug oxidation activities in liver microsomes of various animal species including rats, guinea pigs, dogs, monkeys, and humans. Arch Toxicol. 1997;71:401-408

103. Nelson DR. Cytochrome P450 and the Individuality of Species. Arch Biochem Biophys. 1999;369:1-10

104. Kreyling WG, Abdelmonem AM, Ali Z, Alves F, Geiser M, Haberl N. et al. In vivo integrity of polymer-coated gold nanoparticles. Nat Nanotechnol. 2015;10:619-623

105. Nel AE, Mädler L, Velegol D, Xia T, Hoek EMV, Somasundaran P. et al. Understanding biophysicochemical interactions at the nano-bio interface. Nat Mater. 2009;8:543-557

106. Li M, Zou P, Tyner K, Lee S. Physiologically based pharmacokinetic (PBPK) modeling of pharmaceutical nanoparticles. AAPS J. 2017;19:26-42

107. Xie Y, Bagby TR, Cohen M, Forrest ML. Drug delivery to the lymphatic system: importance in future cancer diagnosis and therapies. Expert Opin Drug Deliv. 2009;6:785-792

108. Stapleton S, Milosevic M, Allen C, Zheng J, Dunne M, Yeung I. et al. A mathematical model of the enhanced permeability and retention effect for liposome transport in solid tumors. PLoS One. 2013;8:1-10

109. Kobayashi H, Watanabe R, Choyke PL. Improving conventional enhanced permeability and retention (EPR) effects; what is the appropriate target?. Theranostics. 2014;4:81-89

110. Blanco E, Shen H, Ferrari M. Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat Biotechnol. 2015;33:941-951

111. Qin S, Seo JW, Zhang H, Qi J, Curry F-RE, Ferrara KW. An imaging-driven model for liposomal stability and circulation. Mol Pharm. 2010;7:12-21

112. Opitz AW, Wickstrom E, Thakur ML, Wagner NJ. Physiologically based pharmacokinetics of molecular imaging nanoparticles for mrna detection determined in tumor-bearing mice. Oligonucleotides. 2010;20:117-125

113. Hendriks BS, Reynolds JG, Klinz SG, Geretti E, Lee H, Leonard SC. et al. Multiscale kinetic modeling of liposomal doxorubicin delivery quantifies the role of tumor and drug-specific parameters in local delivery to tumors. CPT Pharmacometrics Syst Pharmacol. 2012;1:1-11

114. Dellian M, Yuan F, Trubetskoy VS, Torchilin VP, Jain RK. Vascular permeability in a human tumour xenograft: molecular charge dependence. Br J Cancer. 2000;82:1513-1518

115. Hashizume H, Baluk P, Morikawa S, McLean JW, Thurston G, Roberge S. et al. Openings between defective endothelial cells explain tumor vessel leakiness. Am J Pathol. 2000;156:1363-1380

116. Lin P, Chen J-W, Chang LW, Wu J-P, Redding L, Chang H, Y. et al. Computational and ultrastructural toxicology of a nanoparticle, quantum dot 705, in mice. Environ Sci Technol. 2008;42:6264-6270

117. Liang X, Wang H, Grice JE, Li L, Liu X, Xu ZP. et al. Physiologically based pharmacokinetic model for long-circulating inorganic nanoparticles. Nano Lett. 2016;16:939-945

118. Davda JP, Jain M, Batra SK, Gwilt PR, Robinson DH. A physiologically based pharmacokinetic (PBPK) model to characterize and predict the disposition of monoclonal antibody CC49 and its single chain Fv constructs. Int Immunopharmacol. 2008;8:401-413

119. Hardiansyah D, Ng CM. Two-pore minimum physiologically-based pharmacokinetic model to describe the disposition of therapeutic monoclonal IgG antibody in humans. Pharm Res. 2018;35:47

120. Li Y-F, Chen C. Fate and toxicity of metallic and metal-containing nanoparticles for biomedical applications. Small. 2011;7:2965-2980

121. Harashima H, Iida S, Urakami Y, Tsuchihashi M, Kiwada H. Optimization of antitumor effect of liposomally encapsulated doxorubicin based on simulations by pharmacokinetic/pharmacodynamic modeling. J Control Release. 1999;61:93-106

Author contact

Corresponding author: Prof. Gang Zheng, 101 College Street, PMCRT 5-354, Toronto, Ontario, CANADA, M5G 1L7. 416-581-7666 (Office) gang.zhengca

Received 2019-2-28
Accepted 2019-4-26
Published 2019-5-18

Citation styles

©2024 Ivyspring International Publisher. Terms of use