13.3
Impact Factor
Theranostics 2014; 4(10):960-971. doi:10.7150/thno.9293 This issue Cite
Research Paper
Absorption Reconstruction Improves Biodistribution Assessment of Fluorescent Nanoprobes Using Hybrid Fluorescence-mediated Tomography
1. Department of Experimental Molecular Imaging, University Clinic and Helmholtz Institute for Biomedical Engineering, RWTH Aachen University, Aachen, Germany;
2. Department of Experimental Medicine and Immunotherapy, Institute of Applied Medical Engineering, University Hospital RWTH Aachen, Aachen, Germany;
3. Department of Pharmaceutical Product Development, Fraunhofer Institute for Molecular Biology and Applied Ecology, Aachen, Germany.
4. Department of Pharmaceutics, Utrecht Institute for Pharmaceutical Sciences, Utrecht University, Utrecht, The Netherlands
5. Department of Controlled Drug Delivery, MIRA Institute for Biomedical Technology and Technical Medicine, University of Twente, Enschede, The Netherlands.
6. LuFG Informatik 12, RWTH Aachen University, Aachen, Germany.
Received 2014-4-3; Accepted 2014-5-27; Published 2014-7-26
Abstract
Aim: Fluorescence-mediated tomography (FMT) holds potential for accelerating diagnostic and theranostic drug development. However, for proper quantitative fluorescence reconstruction, knowledge on optical scattering and absorption, which are highly heterogeneous in different (mouse) tissues, is required. We here describe methods to assess these parameters using co-registered micro Computed Tomography (µCT) data and nonlinear whole-animal absorption reconstruction, and evaluate their importance for assessment of the biodistribution and target site accumulation of fluorophore-labeled drug delivery systems.
Methods: Besides phantoms with varying degrees of absorption, mice bearing A431 tumors were imaged 15 min and 48 h after i.v. injection of a fluorophore-labeled polymeric drug carrier (pHPMA-Dy750) using µCT-FMT. The outer shape of mice and a scattering map were derived using automated segmentation of the µCT data. Furthermore, a 3D absorption map was reconstructed from the trans-illumination data. We determined the absorption of five interactively segmented regions (heart, liver, kidney, muscle, tumor). Since blood is the main near-infrared absorber in vivo, the absorption was also estimated from the relative blood volume (rBV), determined by contrast-enhanced µCT. We compared the reconstructed absorption with the rBV-based values and analyzed the effect of using the absorption map on the fluorescence reconstruction.
Results: Phantom experiments demonstrated that absorption reconstruction is possible and necessary for quantitative fluorescence reconstruction. In vivo, the reconstructed absorption showed high values in strongly blood-perfused organs such as the heart, liver and kidney. The absorption values correlated strongly with the rBV-based absorption values, confirming the accuracy of the absorption reconstruction. Usage of homogenous absorption instead of the reconstructed absorption map resulted in reduced values in the heart, liver and kidney, by factors of 3.5, 2.1 and 1.4, respectively. For muscle and subcutaneous tumors, which have a much lower rBV and absorption, absorption reconstruction was less important.
Conclusion: Quantitative whole-animal absorption reconstruction is possible and can be validated in vivo using the rBV. Usage of an absorption map is important when quantitatively assessing the biodistribution of fluorescently labeled drugs and drug delivery systems, to avoid a systematic underestimation of fluorescence in strongly absorbing organs, such as the heart, liver and kidney.
Keywords: Fluorescence-mediated Tomography, Diffuse Optical Tomography, Micro-Computed Tomography, Multimodal Imaging, Drug delivery, Nanomedicine.
Introduction
Biodistribution assessment is an essential procedure during drug development to determine the off-target accumulation and the clearance rate [1-4]. To achieve this, organs and tissues are excised from lab mice at different time points and analyzed, which is laborious, expensive and involves the use of many mice. Theranostic drugs include a signaling moiety to allow the use of imaging devices to assess the localization of the probe in vivo. In this way, the mice can get scanned repeatedly, which reduces the number of required animals. Furthermore, data from the same subject is generated, which is statistically more powerful. Nuclear methods, such as Positron emission tomography (PET), provide high accuracy and sensitivity; however, the chemical synthesis is often complicated and requires special equipment. As an alternative, theranostic concepts can be evaluated using preclinical optical imaging methods, which are favored because of their low cost, ease of use, high throughput and the absence of radioactivity [1,4]. Most frequently, planar optical reflectance imaging is used, which has the disadvantage of not being quantitative, surface weighted and almost unusable for longitudinal biodistribution studies. Fluorescence-mediated tomography (FMT) has the potential to overcome these limitations, since it is a tomographic and theoretically quantitative imaging method [5,6]. Furthermore, a rich variety of fluorescent probes is available, allowing imaging of proteolysis, apoptosis, and angiogenesis among others [7-11], which can be applied to noninvasively monitor tumor progression, metastasis, and treatment response [12-14]. Additionally, imaging of gene expression is possible using transgenic reporter mice or cells [5].
Fluorescence reconstruction requires modeling of the photon behavior inside the highly scattering and absorbing tissue. The Born normalization, which is commonly used for fluorescence reconstruction [6], compensates for incorrect assumptions of absorption and scattering for only some configurations as was shown in computer simulations and phantom studies [15-17]. However, accurate fluorescence reconstruction requires knowledge of the true absorption and scattering parameters [15,16,18]. The optical absorption in vivo (Table 1) is strongly determined by the presence of blood, because the absorption of hemoglobin is much higher than other constituents in most tissues [19]. The relative blood volume (rBV) varies strongly in between different tissues, e.g. 2% for muscle, 30% for liver or 100% for pure blood. Therefore, the absorption is highly heterogeneous in vivo, differing locally by orders of magnitude. Since probes are usually injected intravenously, the case of fluorescence being co-localized to strongly absorbing regions, such as blood, liver and kidneys, is highly relevant, particularly for drugs with long blood circulation and hepatic metabolization.
Absorption levels of blood at different wavelengths, corresponding to routinely used FMT channels. Values are based on measurements reported in [51]. Mixed blood assumes 80% venous and 20% arterial blood.
| Channel | Venous | Arterial | Mixed |
|---|---|---|---|
| 635 nm | 9.52 cm-1 | 3.19 cm-1 | 8.26 cm-1 |
| 670 nm | 5.59 cm-1 | 1.84 cm-1 | 4.84 cm-1 |
| 745 nm | 3.71 cm-1 | 2.61 cm-1 | 3.49 cm-1 |
| 790 nm | 4.26 cm-1 | 4.06 cm-1 | 4.23 cm-1 |
For our study, we decided to use a commercially available and widely used FMT [2,10,20-23]. The imaging performance of FMT can get greatly enhanced by combining it with an anatomical modality, such as µCT [24]. The outer shape of the mouse is essential for reconstruction and can be derived from the µCT data [23,24]. A possibly automated segmentation of tissue classes [25] can be used in combination with class-specific absorption and scattering coefficients to derive absorption and scattering maps [7,16], similar as in PET-MR attenuation correction [26]. Unfortunately, strongly absorbing regions such as large blood vessels, the liver, spleen or kidneys, are difficult to segment from native µCT scans due to the low soft-tissue contrast. Furthermore, the blood-perfusion and therefore the absorption are heterogeneous within organs and depend on the metabolic state and pathologies such as anemia. Fortunately, many tissue regions that differ in scattering, e.g. fat, skin, lung and bones, can be segmented from native µCT scans [25] and can be used to derive a scattering map using known tissue specific scattering coefficients [19].
The applicability of FMT for in vivo biodistribution determination is not widely established. Initial results were reported using a standalone FMT [27], however, problems such as dislocated signal became apparent through the combination with µCT [2,22,23]. Furthermore, co-registered anatomical data is beneficial for user-independent multi-organ analysis [2].
The aim of our study is to improve the value of µCT-FMT for bio-distribution assessment. We derive a scattering map from the µCT-based segmentation and reconstruct a whole-animal absorption map from the FMT measurements. Our proposed concept of using a µCT blood-pool contrast agent enables validation of the whole-animal absorption reconstruction in vivo, for the first time, to the best of our knowledge. We show that usage of an absorption map is required to avoid systematic underestimation of fluorescence in strongly absorbing organs such as the heart, liver and kidney. Since these are relevant organs for many intravenously injected drugs, we believe that our method is an important step towards quantitative assessment of the bio-distribution of fluorescent diagnostic and theranostic drugs using µCT-FMT.
Materials and Methods
Approach
After sequential µCT-FMT imaging, the µCT images were automatically segmented to find markers built into the mouse bed for automated fusion. Furthermore, an automated segmentation of the outer shape and of several tissue regions for the scattering map was generated. The whole-animal absorption map was reconstructed by iterative minimization of the difference between predicted and measured excitation boundary values. The absorption reconstruction and the effect on the fluorescence reconstruction were evaluated using phantom experiments. In vivo, the whole-animal absorption reconstruction was validated using the µCT-derived relative blood volume, because the latter is known to essentially determine the absorption in many organs. In the next step, the influence of heterogeneous absorption and scattering maps on the fluorescence reconstruction was investigated. For these experiments, a representative fluorescent polymeric nanocarrier with prolonged circulation time and passive tumor accumulation properties was used [2,20,22].
Hybrid µCT-FMT Imaging
Phantoms and mice were imaged subsequently in µCT (Tomoscope DUO, CT-Imaging, Erlangen, Germany) and FMT (FMT2500, PerkinElmer, Waltham, USA) [2,28]. The FMT uses a thermoelectrically-cooled back-illuminated 16 bit CCD camera (512x512 pixels, CCD size 12.3x12.3 mm). Whole-body FMT scans were acquired at excitation wavelength 745 nm using 100-120 equidistant excitation positions (3 mm distance), covering the body from neck to tail. The control software of the FMT places the laser points so that all laser points are hitting the mouse to avoid damaging the camera. During scanning, the excitation laser power and exposure time are set as high as possible without oversaturating the detector. For a representative scan, this results in exposure times between 30 ms and 1278 ms (mean 180 ms, standard deviation 244 ms). The scanning duration was 5 minutes for µCT and around 15 minutes for FMT. For phantoms, 80-100 scan points were used. After the first FMT scan, the mouse bed, which tightly holds the mouse, was flipped vertically in the FMT to acquire a second scan, providing additional data for reconstruction. All experiments were performed using the same FMT and µCT.
Segmentation used for the scattering map. Several tissue classes that differ in optical scattering were automatically segmented from the µCT data. Fixed scattering coefficients were assigned to these tissue classes to generate a scattering map. (A) Transversal slice through the neck region, showing skin (orange), bones (champagne), fat (blue) and other tissue (light blue). (B) Slice through the lung (purple). (C) Slice through the hip and the tumor (arrow). (D) 3D rendering of the segmentation.
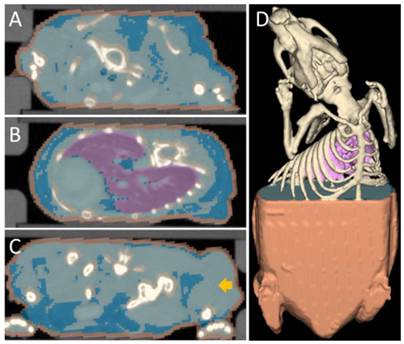
Scattering Map
To derive a scattering map for mouse bodies, several tissue regions (lungs, bones, fat, soft tissue, and skin) were automatically segmented based on the µCT data, similar to the approach in [25] (Figure 1). The algorithm roughly proceeds as follows: First, it segments the skin using a morphologic erosion operation of 2 voxels (voxel size 0.28 mm), starting from the outer shape of the mouse. Then the bones are segmented using a threshold (above 600 HU) and subsequent dilation (1 voxel). To segment the lung, another threshold (-200 HU) is applied. Subsequently, the lung is segmented as the largest connected component of these voxels. Finally, the voxels below 0 HU are classified as fat. The scattering coefficients used for the tissue classes (Table 2) were derived from a recent review [19]. More precisely, we used the scattering coefficients from table 2 in combination with formula 1 from [19].
Scattering coefficients used for the scattering map (at wavelength 745nm). Values are based on measurements reported in [19].
| Tissue | Scattering |
|---|---|
| Lung | 20.5 cm-1 |
| Other | 11.2 cm-1 |
| Bones | 17.1 cm-1 |
| Skin | 25.9 cm-1 |
| Fat | 14.0 cm-1 |
Absorption Reconstruction
The absorption map was reconstructed using model based iterative image reconstruction [29]. The optical forward model was implemented using a finite difference mesh (mesh size 0.56mm) which approximates the diffusion equation [30]. This results in a sparse symmetric positive matrix 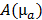 , which depends on the absorption map
, which depends on the absorption map 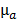 and the fixed pre-determined scattering map. The three-dimensional absorption map
and the fixed pre-determined scattering map. The three-dimensional absorption map  , treated as a flattened vector, was reconstructed by iteratively minimizing a differentiable nonlinear cost function
, treated as a flattened vector, was reconstructed by iteratively minimizing a differentiable nonlinear cost function 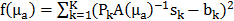 expressing the squared difference between predicted and measured boundary values for all
expressing the squared difference between predicted and measured boundary values for all 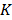 source points. To compensate for the high dynamic range of the measurements, the relative difference was used for bright measurements above a pre-determined threshold. The source maps
source points. To compensate for the high dynamic range of the measurements, the relative difference was used for bright measurements above a pre-determined threshold. The source maps 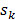 were modeled as Gaussian distributions. To decouple the degrees of freedom from the meshing accuracy, the absorption map was expressed in terms of nonnegative equidistant Gaussian basis functions. Boundary measurements
were modeled as Gaussian distributions. To decouple the degrees of freedom from the meshing accuracy, the absorption map was expressed in terms of nonnegative equidistant Gaussian basis functions. Boundary measurements 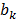 were determined by projecting the pixels from the camera onto the mouse surface.
were determined by projecting the pixels from the camera onto the mouse surface. 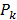 is the linear operator that extracts the observable boundary values from the computed excitation maps. The cost function
is the linear operator that extracts the observable boundary values from the computed excitation maps. The cost function 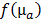 was minimized with respect to the absorption map using the nonlinear conjugate gradient method and the required gradient computations were performed using algorithmic differentiation [31,32] with GPU-accelerated sparse vector and matrix operations [33]. The unknown scale factor between source power and pixel intensities was calibrated using a phantom with known homogeneous scattering (8 cm-1) and negligible absorption (0.1 cm-1). Minimization of the cost function results in quantitative absorption values and further calibration, e.g. using a probe with known absorption, is not required.
was minimized with respect to the absorption map using the nonlinear conjugate gradient method and the required gradient computations were performed using algorithmic differentiation [31,32] with GPU-accelerated sparse vector and matrix operations [33]. The unknown scale factor between source power and pixel intensities was calibrated using a phantom with known homogeneous scattering (8 cm-1) and negligible absorption (0.1 cm-1). Minimization of the cost function results in quantitative absorption values and further calibration, e.g. using a probe with known absorption, is not required.
Fluorescence Reconstruction
Using the scattering and absorption maps, the fluorescence distribution was reconstructed. This was performed by utilizing the normalized Born ratio and computing a dense weight matrix 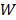 [4,7,24], from which the fluorescence distribution
[4,7,24], from which the fluorescence distribution 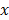 was reconstructed by non-negative least squares minimization of
was reconstructed by non-negative least squares minimization of 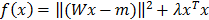 , where
, where 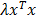 is a regularization term to avoid degenerate solutions. Furthermore, the fluorescence was expressed in terms of nonnegative equidistant Gaussian basis functions (spacing 1.12 mm, standard deviation 1.12 mm). To solve the least squares system, GPU-accelerated multiplicative updates were used, a method with high performance and guaranteed non-negative solutions [34]. The same mesh size as for the absorption reconstruction was used. Fluorescence was reconstructed using three configurations. First, heterogeneous absorption and heterogeneous scattering were used. Second, only the absorption map was replaced with a homogeneous absorption map (constant value of 0.3 cm-1). Third, only the scattering map was replaced using homogeneous scattering (constant value of 11.2 cm-1 from Table 1). For the in vivo experiments, the calibration factors were determined using phantom scans and a known amount of fluorescence.
is a regularization term to avoid degenerate solutions. Furthermore, the fluorescence was expressed in terms of nonnegative equidistant Gaussian basis functions (spacing 1.12 mm, standard deviation 1.12 mm). To solve the least squares system, GPU-accelerated multiplicative updates were used, a method with high performance and guaranteed non-negative solutions [34]. The same mesh size as for the absorption reconstruction was used. Fluorescence was reconstructed using three configurations. First, heterogeneous absorption and heterogeneous scattering were used. Second, only the absorption map was replaced with a homogeneous absorption map (constant value of 0.3 cm-1). Third, only the scattering map was replaced using homogeneous scattering (constant value of 11.2 cm-1 from Table 1). For the in vivo experiments, the calibration factors were determined using phantom scans and a known amount of fluorescence.
Phantom Experiments
A block shaped FMT phantom (33x40x15 mm³, absorption 0.1 cm-1, scattering 8 cm-1), containing a cylindrical inclusion (diameter 3 mm, length 1 cm, 3 mm below the surface), was scanned with varying concentrations of absorptive dye (E150, Wusitta, Sitzendorf, Germany) and a constant concentration of fluorescence (OsteoSense750, PerkinElmer, Waltham, USA, excitation peak 750 nm, emission peak 780 nm). To facilitate the segmentation of the inclusion in the µCT images, 5% CT contrast agent (Imeron 400, Bracco Imaging, Konstanz, Germany) was added. Additionally, computer simulations similar to [15] were performed to exclude a systematic error in the physical experiments. For these simulations, the same phantom shape and optical properties were used. The cylindrical inclusion was filled with constant fluorescence and varying absorption levels. Using the optical forward model, the measurable values on the surface were computed for all source points. Subsequently, the fluorescence was reconstructed using homogeneous and heterogeneous absorption maps.
To assess the sensitivity of the FMT, we scanned the phantom with an increasingly diluted fluorescence concentration (OsteoSense750). The contrast-to-noise (CNR) ratio was determined to find the lowest concentration where the inclusion could be clearly distinguished from the background noise (CNR greater 4).
Absorption of Blood
Optical absorption of venous and arterial blood was determined for the four FMT channels of our device (Table 1) using measured absorption values of oxyhemoglobin and deoxyhemoglobin reported in [19,35]. We assumed a hemoglobin concentration in blood of 150 g/l, which is realistic for mice [36]. Furthermore, we assumed venous and arterial oxygenation levels of 70% and 98%, respectively. For mixed blood 80% venous and 20% arterial blood was assumed.
Animal Experiments
All experimental procedures were approved by the local and national animal experiments ethics committee and conducted according to their regulations. BALB/c nu/nu mice bearing a A431 tumor in the right hind limb were imaged by µCT-FMT directly and at 48 h after i.v. injection of a µCT blood pool contrast agent (50 µl, ExIA160XL, Binitio, Ottawa, USA), as well as 40 µl (2 nmol) of a prototypic pHPMA-based polymeric drug carrier labeled with the near-infrared fluorophore Dy750 (Dyomics GmbH, Jena, Germany) [2]. Five mice were imaged, but one mouse died before imaging at 48 h.
Image Analysis
Several organs (heart, liver, kidneys, muscle and tumor) were interactively segmented based purely on the µCT data using the Imalytics Preclinical Software (developed at ExMI, Aachen, Germany, in cooperation with Philips Research, Aachen, Germany). The relative blood volume (rBV) of these organs was determined based on the ratio between organ and blood enhancement created by the µCT blood pool agent [37,38]. For these organs, an average absorption value was estimated from the rBV, the absorption of mixed blood (Table 1) and assuming negligible absorption for unperfused tissue [19]. Using the organ segmentations, the average values of reconstructed absorption and reconstructed fluorescence concentration of the organs were determined.
Statistical Analysis
Pearson correlation analysis was used for the phantom experiments and to correlate the reconstructed absorption with the rBV-based absorption of organs. Differences between fluorescence concentrations of organs (reconstructed using heterogeneous and homogenous absorption) were shown using a paired two-tailed t-test including Bonferroni correction.
Results
Phantoms
To evaluate the absorption reconstruction under reproducible conditions, we used phantoms containing an inclusion with fluorescent and absorptive dyes. We imaged phantoms with identical fluorescence but varying absorption, which simulates the case of fluorescence in highly or weakly blood-perfused, and therefore more or less optically absorbing, regions. The reconstructed absorption appeared in or at least near to the inclusion (Figure 2A,B) and correlated strongly with the dilution of the absorptive dye (R²=0.99, P<0.001), showing that the 3D absorption could be reconstructed quantitatively. Furthermore, the fluorescence concentration was reconstructed. First, the fluorescence was reconstructed assuming homogeneous absorption maps. Strong absorption caused significant underestimation of the reconstructed fluorescence (Figure 2C,D). This effect was negligible for low absorption values (e.g. below 0.6 cm-1), which confirms the results of previous simulation studies [15,16], which ignored cases with stronger absorption. The underestimation of fluorescence did also occur when using the fluorescence reconstructed by the FMT system, which we registered with the µCT data, indicating that this phenomenon is not dependent on our fluorescence reconstruction implementation. Our observed underestimation of fluorescence for strong co-localized absorption is explainable because the effect of absorption is stronger on the emission measurements than on the excitation measurements (Figure 3). Therefore, these differences are not canceled completely by computing the ratio. The fluorescence reconstruction, which receives the ratio as input only, explains the measurements with low fluorescence, resulting in the observed underestimation. By using the reconstructed heterogeneous absorption map for fluorescence reconstruction, the underestimation could be decreased (Figure 2D), indicating that an absorption map is useful for quantitative fluorescence reconstruction in realistic scenarios with high absorption. To show that these observations are not caused by experimental errors, we performed computer simulations, which resemble our lab experiments with respect to the phantom shape and the absorption levels. In the simulations, virtual measurements were created based on assumed fluorescence and absorption as described in [15]. Then the fluorescence was reconstructed assuming homogenous and heterogeneous absorption maps. The results of these simulations confirmed our experimental results (Figure 2F), showing that low absorption values have little impact on the fluorescence reconstruction, however, that strong absorption causes significant underestimation of co-localized fluorescence.
We also performed phantom experiments to determine the sensitivity of the FMT, which showed that, using either reconstruction method, concentrations down to 42 nM, i.e. 4.2 pmol inside the 100 µl region, could be distinguished from the background noise.
Absorption in vivo
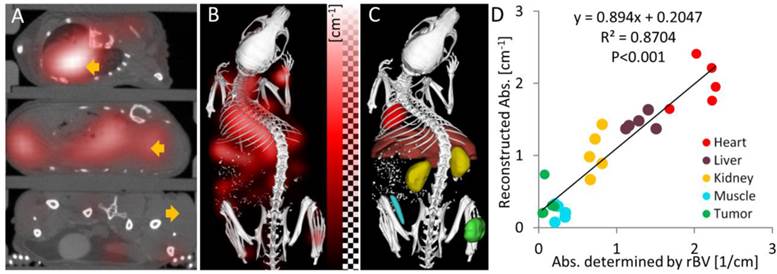
To evaluate the absorption reconstruction in vivo, we analyzed the reconstructed absorption of organs and tumors in mice. For this analysis, several tissue regions (heart, liver, kidney, muscle, tumor) were segmented based on the µCT data. The reconstructed absorption values were high for heart (2.00 ± 0.32 cm-1), liver (1.45 ± 0.11 cm-1) and kidney (1.04 ± 0.30 cm-1), i.e. they were higher than 0.6 cm-1 which was the assumed maximum value in previous simulation studies [15,16]. It was relatively low for muscle (0.21 ± 0.10 cm-1) and tumor (0.35 ± 0.22 cm-1). Strong absorption was also evident in the camera images acquired during the excitation pass, which showed almost complete extinction close to the heart. We also determined the relative blood volume (rBV) in these regions using contrast enhanced µCT, which is possible, because the long circulating µCT contrast agent resides in the blood immediately after injection [37,38]. The rBV was computed as the ratio between organ enhancement and blood enhancement, which were determined using the interactive segmentation. In the chosen regions, the relative blood volume dominates the near-infrared absorption [19], which enables validation of the absorption reconstruction in vivo. We estimated the absorption from the rBV using the known absorption of blood (3.49 cm-1) at the used wavelength 745 nm (Table 1). The reconstructed absorption values were similar to the rBV-based absorption and correlation analysis showed a strong and significant correlation (R²=0.87, P<0.001, Figure 4). The slope of the regression line (slope=0.89) was relatively close to 1, showing that the absorption could be reconstructed quantitatively.
Fluorescence in vivo
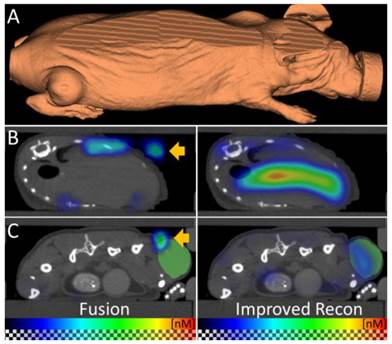
To apply µCT-FMT for biodistribution assessment of a typical theranostic agent, we used a customizable fluorescent nanopolymer suitable for image-guided passive and active tumor-targeted drug delivery [2,20]. The mice were imaged directly and 48h after i.v. injection. First, we compared the FMT reconstruction of the vendor with our newly implemented fluorescence reconstruction. The FMT assumes a block-shaped mouse, which causes artifacts such as dislocated signal outside the mouse, which become apparent after fusion with the µCT data (Figure 5). Our reconstruction, which uses the shape derived from the µCT for optical modeling, avoids these problems. Therefore, we only used our reconstructions for analysis during this study.
Phantom experiments. (A) Phantoms with a cylindrical inclusion filled with constant fluorescence and increasing absorptive dye concentrations. The reconstructed absorption appears correctly in the inclusion and is proportional to the absorptive dye concentration (B). (C) The reconstructed fluorescence appears in the inclusion but is suppressed by strong absorption when assuming homogeneous absorption, resulting in a strong negative correlation (D). Usage of the reconstructed heterogeneous absorption avoids this underestimation. Computer simulations using the same phantom shape (E) support the experimental results (F), showing that an absorption map is required to avoid underestimation of fluorescence in absorbing regions.
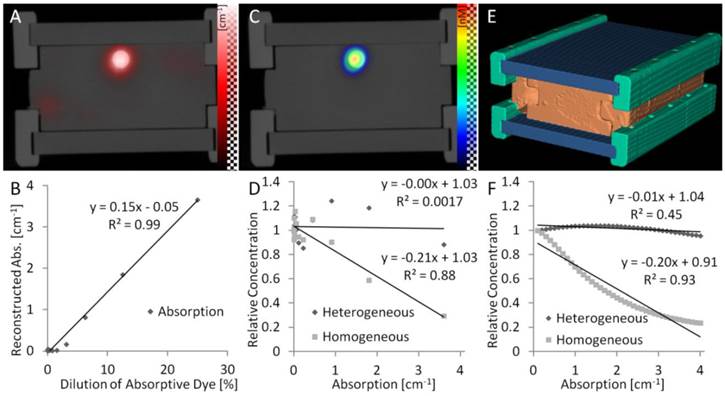
Co-localized absorption and fluorescence. In this phantom, absorption and fluorescence are co-localized in a small cylindrical inclusion (arrow). The laser source is shown on the bottom. The absorption has a different effect on the excitation and emission measurements. For the excitation measurements (A), some photons pass through the absorption and some pass around the absorption, before reaching the surface where it is measured. For the emission measurements (B), all photon paths reaching the surface go through the absorbing region, where the fluorescence is located in this example. Therefore, the ratio of emission and excitation measurements does not cancel out the effect of heterogeneous absorption, which becomes apparent in the ratio images as seen from the camera (C).
Absorption reconstruction in vivo. (A) Axial slices through the heart, liver and tumor (arrows) showing the absorption as red overlay. High absorption appears in the heart and the liver while the absorption in the tumor is low. (B) 3D rendering shows high absorption in the upper torso, where the heart and the liver reside. (C) Segmented regions (heart, liver, kidney, muscle and tumor) used to quantify the optical absorption. (D) Correlation of reconstructed organ absorption with the absorption determined from the relative blood volume (rBV). The same colors are used for the tissue regions as in (C). The strong correlation shows that the absorption map can be reconstructed quantitatively.
Improved fluorescence reconstruction using the shape. (A) The shape of the mouse is derived from the µCT data and used for accurate optical modeling and reconstruction. The mouse shape does not resemble a block which the standalone-FMT assumes for reconstruction. (B, C) The fused FMT reconstruction (left) is compared to the improved reconstruction (right) for transversal slices through liver and tumor, 48 h after injection of the nanopolymer. (B) Absence of the shape information results in erroneous signal in the air (arrow). Usage of the shape for reconstruction avoids this problem. (C) Fusion shows dislocated signal (arrow) above the tumor (green) which is corrected by using the shape for reconstruction. These examples show the importance of the shape information for fluorescence reconstruction.
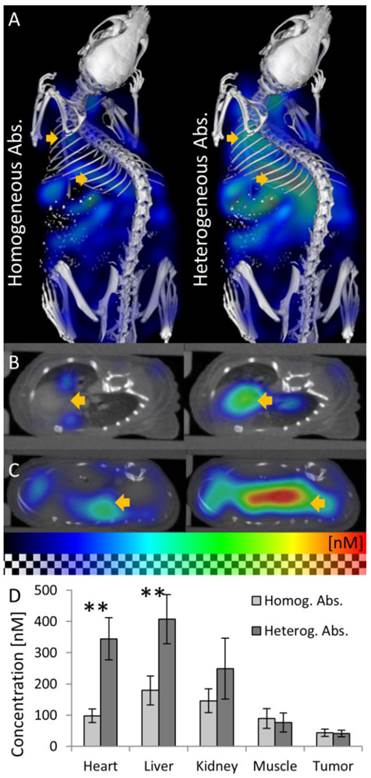
Effect of absorption on fluorescence in vivo. The effect of using homogeneous or heterogeneous absorption on the fluorescence reconstruction is analyzed 15 min after i.v. injection of a long circulating fluorescence-labeled nanocarrier designed for passive tumor accumulation. (A) 3D renderings of reconstructed fluorescence distribution. Left: Reconstruction using homogeneous absorption. Right: Reconstruction using heterogeneous absorption. Both reconstructions use the shape information. High signal is expected in well-perfused organs such as heart, liver and kidneys shortly after i.v. injection. (B) Transversal slice through the heart (arrow). Only when using heterogeneous absorption (right), the expected strong signal in the heart is reconstructed. (C) Slice through the liver. (D) Fluorescence after injection is significantly (P<0.01) lower in strongly absorbing organs such as heart and liver when assuming homogenous absorption.
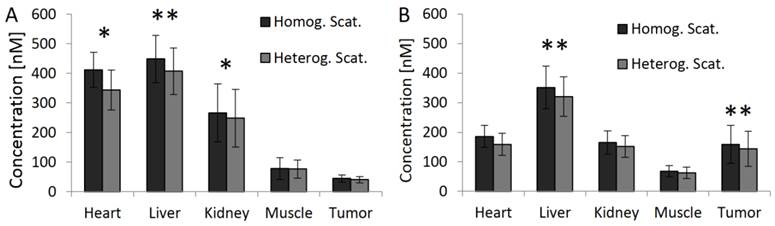
Fluorescence in vivo 48h after injection. (A) 3D renderings of reconstructed fluorescence distribution. Left: Reconstruction using homogeneous absorption. Right: Reconstruction using heterogeneous absorption. High signal appears in the liver and tumor (arrows). (B) Transversal slice through the liver (arrow). (C) Slice through the subcutaneous tumor (arrow), 48 h after i.v. injection, showing high fluorescence concentration caused by passive probe accumulation. (D) Usage of the absorption map avoids underestimation of fluorescence in strongly absorbing organs such as heart and liver but hardly affects muscle and tumor (* indicates P<0.05).
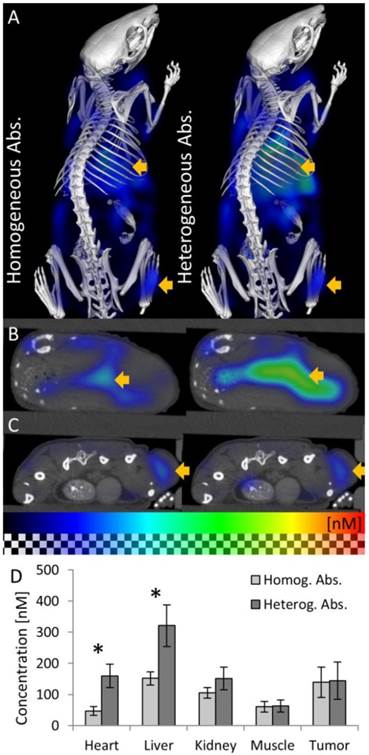
We reconstructed the fluorescence using the heterogeneous scattering and absorption maps. At the early time point where the agent mostly resides in the blood circulation, high fluorescence was detected at well-perfused organs such as heart, liver and kidneys (Figure 6). 48 h after injection, the fluorescence decreased in heart, liver, kidney and muscle (Figure 7). The signal in the tumor increased significantly (P<0.05) from 40 ± 10 nM to 144 ± 59 nM, due to the expected passive accumulation through leaky blood vessels (Figure 7). To assess the effect of the heterogeneous absorption map, the fluorescence was also reconstructed using homogenous absorption. The same heterogeneous scattering map was used, which had been derived from the µCT-based segmentation and tissue specific scattering coefficients (Table 2). The fluorescence in the tumor increased from 43 ± 12 nM to 139 ± 49 nM, P<0.05, similar to the absorption-corrected method. Therefore, the absorption correction only had a minor effect on the tumor. In strongly absorbing organs, such as heart, liver and kidney, a systematic difference was observed, however. When assuming homogenous absorption, the reconstructed fluorescence was reduced by a factor 3.5 ± 0.6 for the heart, by 2.1 ± 0.3 in the liver and by 1.4 ± 0.4 in the kidney. These differences were significant for heart and liver but not for kidney, muscle and tumor. The suppressed liver signal caused a significantly (P<0.05) higher tumor to liver ratio (0.93 ± 0.37 vs. 0.47 ± 0.24 using absorption correction), showing that the assumption of homogenous absorption causes overoptimistic estimates of the tumor-to-liver ratio.
Next to analyzing the influence of the absorption map on the fluorescence quantification, we also investigated the effect of different scattering maps for fluorescence reconstruction. Compared to absorption, usage of a scattering map had less of an effect for whole-animal scans (Figure 8). This is reasonable, because the absorption varies much more between organs due to the strongly varying relative blood volume.
Discussion
The aim of our study was to improve the applicability of FMT for quantitative bio-distribution assessment. To this end, we investigated the necessity of absorption modeling for fluorescence reconstruction. Phantom and in vivo experiments showed that the spatial absorption map can be reconstructed quantitatively, and its usage for fluorescence reconstruction is essential to avoid underestimation of fluorescence in strongly absorbing regions. Underestimation of fluorescence in absorbing regions might sound obvious, but it is not, since the normalized born ratio is intended to and capable of correcting incorrect absorption modeling. This was shown in computer simulations and phantom studies for cases of low absorption or when the absorption is distant to the fluorescence [15-17]. However, this seems not to be true for co-localization of fluorescence and strong absorption.
A reasonable absorption map is difficult to derive from native µCT scans because liver, spleen and kidney are difficult to be segmented automatically. Blood vessels, which strongly determine the absorption, are even more difficult to be segmented, because blood is hardly distinguishable from other soft tissues such as muscle. Therefore, we used the µCT data to estimate a scattering map using automated segmentation of tissue regions such as bones, fat, and the lung. Instead of relying on an error-prone automated or manual segmentation to derive the absorption map, we reconstructed the absorption map from the optical raw data. It is difficult to validate the absorption reconstruction by analyzing excised organs, because the blood coagulates, deoxygenates or flows out of the organs. Therefore, we validated the absorption reconstruction in vivo using the µCT-derived relative blood volume, which is applicable because blood is the dominant absorber in these organs [19,35], and oxygenated and deoxygenated hemoglobin have similar absorption at the chosen wavelength (Table 1). An alternative method to derive an absorption map could be to use an iodine-based µCT blood pool contrast agent in combination with dual energy µCT imaging for blood vessel segmentation [39]. However, for routine µCT-FMT imaging, the use of µCT contrast agent is problematic for reasons of handling and toxicity. Furthermore, a steady state of µCT contrast enhancement is hardly achievable for longitudinal imaging, because the µCT contrast agent has its own dynamic bio-distribution.
Effect of scattering map. The effect of using homogenous and heterogeneous scattering on the fluorescence reconstruction was compared. The heterogeneous scattering map is derived from the µCT-based segmentation. Both methods perform absorption reconstruction. (A) Fluorescence 15 min after injection. (B) Fluorescence 48h after injection. Assuming homogenous scattering results in slight overestimation of fluorescence in all regions (* indicates P<0.05 and ** indicates P<0.01).
Absorption reconstruction is a nonlinear problem, particularly for strong absorption [40], requiring a computationally demanding iterative method [29,41]. Due to the computational load, previous studies were often restricted to 2D configurations [42] or small fields-of-view [40]. To perform 3D reconstructions of whole animals, we compute the gradients using algorithmic differentiation [32] with GPU-accelerated sparse vector and matrix operations [33], where the derivatives are propagated backwards through a linear solver [31] at each iteration. This approach could be extended to use multispectral data or to include the emission channel to potentially allow reconstruction of absorption and scattering which is not generally possible using a single trans-illumination channel [43]. The convergence of the nonlinear reconstruction could be improved using Quasi-Newton methods [42] compared to the robust and simple nonlinear conjugate gradient method which we currently use.
In our study, we performed whole-body scans resulting in coarse laser source points (3 mm distance), limiting the achievable resolution of reconstructed absorption and fluorescence. This could be improved by increasing the number of measurement points (and the measurement time), by restricting imaging to a smaller part of the body or by using the segmentation for regularization for the fluorescence reconstruction [7,23]. To increase the number of measurements, we combined up and down scans into one reconstruction, which can be further increased using 360° systems [24]. However, the benefit of 360° is not as important as in computed tomography where real projections are acquired, because for diffuse optical imaging only viewing-angle-independent surface measurements are obtained. Our approach can be used with other continuous wave FMT systems as long as µCT data is available to derive the outer shape and a scattering map. While reconstruction of absorption and scattering may be feasible under certain conditions [44], we derived the scattering map through a segmentation, which reduces the number of free parameters and also avoids the issue of ambiguity [43]. Our segmentation-based scattering map is not perfect, however, because some regions, e.g. stomach contents, are omitted, and, in reality, the scattering is not homogeneous within the segmented regions. Nevertheless, we show that using heterogeneous scattering maps has less of an effect for fluorescence reconstruction than using heterogeneous absorption maps. While this differs from previous results [15], our results are explainable because for whole-animal scans the absorption is much stronger and varies much more than anticipated in these computer simulations.
Currently, we can only show that the absorption map makes a relevant difference for the fluorescence reconstruction in vivo. To achieve a quantitative validation of the fluorescence reconstruction in vivo, dual-tracer imaging (nuclear and fluorescent) would be a good solution [45-47]. Furthermore, the fluorescence signal in the heart appears lower than expected when compared to the liver. One reason may be that strong absorption leads to a loss of many measurement points close to the heart, because the measured excitation light has to be well above the noise level to be used for the normalizing ratio [48]. This could be overcome by increasing the exposure time in combination with high dynamic range imaging. Furthermore, the strong absorption in some regions may justify use of the more complex radiative transfer equation (RTE) instead of the diffusion equation [49], because the latter assumes that absorption is well below scattering. Photoacoustic imaging could be an alternative modality to compute an absorption map, if quantitative reconstruction issues and problems with the special acoustic properties of lungs and bones can be resolved [50]. Not only for fluorescence reconstruction, but also for other optical imaging techniques, e.g. quantitative bioluminescence reconstruction [48], the availability of a whole-animal absorption map could be useful. Furthermore, by using multispectral imaging, i.e. absorption reconstruction in several wavelengths, the tissue oxygenation could be determined.
We found that the reconstructed fluorescence in the subcutaneous tumor is hardly affected by absorption modeling, which is in line with previously reported results where strong absorption was positioned around the fluorescence [17]. For experiments with tumors that contain hemorrhages or melanin an absorption map should be used, however. Furthermore, the phenomenon of fluorescence underestimation in the liver may cause overoptimistic estimates for the tumor-to-liver ratio, which can be used to assess the efficacy of tumor targeted drugs [2], by roughly a factor two. Consequently, proper absorption modeling should be used for such studies, because otherwise, it might lead to inaccurate conclusions. Compared to the other available FMT channels, the channel at 745 nm has lowest absorption for mixed blood (Table 1) and, therefore, the observed effects should be even stronger in the other channels.
In conclusion, our results indicate that the absorption map can be reconstructed quantitatively from the optical raw data when assuming that an approximate scattering map is available. Our novel approach of using contrast-enhanced µCT to determine the relative blood volume is an essential step to evaluate the absorption reconstruction in vivo. We show that an absorption map is required to avoid strong and systematic underestimation of fluorescence in highly absorbing regions, such as the heart, liver and kidneys. Therefore, absorption should be reconstructed and used when the bio-distribution is to be determined quantitatively using FMT. Since bio-distribution assessment is necessary to characterize the excretion pathways and to exclude unwanted accumulation sites, we believe that our results are an important step towards establishing µCT-FMT as a valuable tool for diagnostic and theranostic drug development.
Abbreviations
FMT: Fluorescence-mediated Tomography; µCT: Micro-Computed Tomography; rBV: relative Blood Volume; CW: Continuous Wave.
Acknowledgements
We thank Marek Weiler for performing the phantom experiments. This work was supported by the European Research Council (ERC Starting Grant 309495: NeoNaNo), the European Commission (FP7: COST-Action TD1004: Nanotheragnostics), the German Federal State of North Rhine Westphalia (NRW; High-Tech.NRW/EU-Ziel 2-Programm (EFRE); ForSaTum), the German Research Foundation (DFG: La2937/1-2), RWTH Aachen University (I3TM Seed Fund) and Philips Research (Aachen, Germany).
Competing Interests
Felix Gremse is founder and owner of Gremse-IT, a startup company that offers software and services for medical image analysis in cooperation with Philips and the Department for Experimental Molecular Imaging of the RWTH Aachen University.
References
1. Baker M. Whole-animal imaging: The whole picture. Nature. 2010;463(7283):977-80
2. Kunjachan S, Gremse F, Theek B. et al. Noninvasive optical imaging of nanomedicine biodistribution. ACS Nano. 2013;7(1):252-62
3. Licha K, Olbrich C. Optical imaging in drug discovery and diagnostic applications. Adv Drug Deliv Rev. 2005;57(8):1087-108
4. Stuker F, Ripoll J, Rudin M. Fluorescence Molecular Tomography: Principles and Potential for Pharmaceutical Research. Pharmaceutics. 2011;3(2):229-74
5. Ntziachristos V. Fluorescence molecular imaging. Annu Rev Biomed Eng. 2006;8:1-33
6. Ntziachristos V, Weissleder R. Experimental three-dimensional fluorescence reconstruction of diffuse media by use of a normalized Born approximation. Opt Lett. 2001;26(12):893-5
7. Ale A, Ermolayev V, Herzog E. et al. FMT-XCT: in vivo animal studies with hybrid fluorescence molecular tomography-X-ray computed tomography. Nat Methods. 2012;9(9):615-20
8. Eisenblätter M, Ehrchen J, Varga G. et al. In vivo optical imaging of cellular inflammatory response in granuloma formation using fluorescence-labeled macrophages. J Nucl Med. 2009;50(10):1676-82
9. Lederle W, Arns S, Rix A. et al. Failure of annexin-based apoptosis imaging in the assessment of antiangiogenic therapy effects. EJNMMI Res. 2011;1:26
10. Nahrendorf M, Waterman P, Thurber G. et al. Hybrid in vivo FMT-CT imaging of protease activity in atherosclerosis with customized nanosensors. Arterioscler Thromb Vasc Biol. 2009;29(10):1444-51
11. Rao J, Dragulescu-Andrasi A, Yao H. Fluorescence imaging in vivo: recent advances. Curr Opin Biotechnol. 2007;18(1):17-25
12. Al Rawashdeh W, Arns S, Gremse F. et al. Optical tomography of MMP-activity allows a sensitive non-invasive characterization of the invasiveness and angiogenesis of SCC-xenografts. Neoplasia. 2014;16(3):235-46
13. Kaijzel EL, van der Pluijm G, Löwik CWGM. Whole-body optical imaging in animal models to assess cancer development and progression. Clin Cancer Res. 2007;13(12):3490-7
14. Li R, Zheng K, Chen Z. et al. A Novel Tumor Targeting Drug Carrier for Optical Imaging and Therapy. Theranostics. 2014;4(6):642-59
15. Abascal JFP-J, Aguirre J, Chamorro-Servent J. et al. Influence of absorption and scattering on the quantification of fluorescence diffuse optical tomography using normalized data. J Biomed Opt. 2012;17(3):036013
16. Hyde D, Schulz R, Brooks D. et al. Performance dependence of hybrid x-ray computed tomography/fluorescence molecular tomography on the optical forward problem. J Opt Soc Am A Opt Image Sci Vis. 2009;26(4):919-23
17. Soubret A, Ripoll J, Ntziachristos V. Accuracy of fluorescent tomography in the presence of heterogeneities: study of the normalized Born ratio. IEEE Trans Med Imaging. 2005;24(10):1377-86
18. Patwardhan SV, Culver JP. Quantitative diffuse optical tomography for small animals using an ultrafast gated image intensifier. J Biomed Opt. 2008;13(1):011009
19. Jacques SL. Optical properties of biological tissues: a review. Phys Med Biol. 2013;58(11):R37
20. Kunjachan S, Pola R, Gremse F. et al. Passive versus Active Tumor Targeting Using RGD- and NGR-Modified Polymeric Nanomedicines. Nano Lett. 2014;14(2):972-81
21. Schober A, Nazari-Jahantigh M, Wei Y. et al. MicroRNA-126-5p promotes endothelial proliferation and limits atherosclerosis by suppressing Dlk1. Nat Med. 2014;20(4):368-76
22. Theek B, Gremse F, Kunjachan S. et al. Characterizing EPR-mediated passive drug targeting using contrast-enhanced functional ultrasound imaging. J Control Release. 2014(182):83-9
23. Radrich K, Ale A, Ermolayev V. et al. Improving limited-projection-angle fluorescence molecular tomography using a co-registered x-ray computed tomography scan. J Biomed Opt. 2012;17(12):126011
24. Schulz RB, Ale A, Sarantopoulos A. et al. Hybrid system for simultaneous fluorescence and x-ray computed tomography. IEEE Trans Med Imaging. 2010;29(2):465-73
25. Freyer M, Ale A, Schulz RB. et al. Fast automatic segmentation of anatomical structures in x-ray computed tomography images to improve fluorescence molecular tomography reconstruction. J Biomed Opt. 2010;15(3):036006
26. Keereman V, Mollet P, Berker Y. et al. Challenges and current methods for attenuation correction in PET/MR. MAGMA. 2013;26(1):81-98
27. Vasquez KO, Casavant C, Peterson JD. Quantitative Whole Body Biodistribution of Fluorescent-Labeled Agents by Non-Invasive Tomographic Imaging. PLoS ONE. 2011;6(6):e20594
28. Doleschel D, Mundigl O, Wessner A. et al. Targeted near-infrared imaging of the erythropoietin receptor in human lung cancer xenografts. J Nucl Med. 2012;53(2):304-11
29. Hielscher AH. Optical tomographic imaging of small animals. Curr Opin Biotechnol. 2005;16(1):79-88
30. Sevick-Muraca EM, Rasmussen JC. Molecular imaging with optics: primer and case for near-infrared fluorescence techniques in personalized medicine. J Biomed Opt. 2008;13(4):041303
31. Davies AJ, Christianson DB, Dixon LCW. et al. Reverse differentiation and the inverse diffusion problem. Adv Eng Softw. 1997;28(4):217-21
32. Naumann U. The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation. Philadelphia, PA, USA: SIAM. 2012:358 p
33. Bell N, Dalton S, Olson LN. Exposing Fine-Grained Parallelism in Algebraic Multigrid Methods. SIAM J Sci Comput. 2012;34(4):C123-C152
34. Lin C-J. On the Convergence of Multiplicative Update Algorithms for Nonnegative Matrix Factorization. IEEE Trans Neural Netw. 2007;18(6):1589-1596
35. Cheong W-F, Prahl SA, Welch AJ. A review of the optical properties of biological tissues. IEEE J Quantum Electron. 1990;26(12):2166-85
36. Goulden F, Warren FL. The Hemoglobin Content of the Blood of Mice of the RIII and CBA Strains. Cancer Res. 1944;4(7):421-4
37. Ehling J, Bartneck M, Wei X. et al. CCL2-dependent infiltrating macrophages promote angiogenesis in progressive liver fibrosis. Gut. 2014
38. Ehling J, Theek B, Gremse F. et al. Micro-CT imaging of tumor angiogenesis: quantitative measures describing micromorphology and vascularization. Am J Pathol. 2014;184(2):431-41
39. Gremse F, Grouls C, Palmowski M. et al. Virtual Elastic Sphere Processing Enables Reproducible Quantification of Vessel Stenosis at CT and MR Angiography. Radiology. 2011;260:709-17
40. Arridge SR, Dorn O, Kolehmainen V. et al. Parameter and structure reconstruction in optical tomography. J Phys: Conf Ser. 2008;135(1):012001
41. Arridge SR, Schotland JC. Optical tomography: forward and inverse problems. Inverse Probl. 2009;25(12):123010
42. Klose AD, Hielscher AH. Quasi-Newton methods in optical tomographic image reconstruction. Inverse Probl. 2003;19(2):387
43. Arridge SR, Lionheart WRB. Nonuniqueness in diffusion-based optical tomography. Opt Lett. 1998;23(11):882-4
44. Harrach B. Simultaneous determination of the diffusion and absorption coefficient from boundary data. Inverse Probl Imaging. 2012;6(4):663-79
45. Culver J, Akers W, Achilefu S. Multimodality Molecular Imaging with Combined Optical and SPECT/PET Modalities. J Nucl Med. 2008;49(2):169-72
46. Garofalakis A, Dubois A, Kuhnast B. et al. In vivo validation of free-space fluorescence tomography using nuclear imaging. Opt Lett. 2010;35(18):3024-6
47. Xing Y, Zhao J, Conti PS. et al. Radiolabeled Nanoparticles for Multimodality Tumor Imaging. Theranostics. 2014;4(3):290-306
48. Ntziachristos V, Ripoll J, Wang LV. et al. Looking and listening to light: the evolution of whole-body photonic imaging. Nat Biotechnol. 2005;23(3):313-20
49. Arridge SR. Optical tomography in medical imaging. Inverse Probl. 1999;15(2):R41
50. Lutzweiler C, Razansky D. Optoacoustic Imaging and Tomography: Reconstruction Approaches and Outstanding Challenges in Image Performance and Quantification. Sensors. 2013;13(6):7345-84
51. Optical absorption of hemoglobin. Prahl S. http://omlc.ogi.edu/spectra/hemoglobin
Author contact
![]() Corresponding author: Dipl.-Inf. Felix Gremse, Experimental Molecular Imaging, RWTH University Aachen, Pauwelsstr. 30, 52074 Aachen, Germany. Phone: +49 241 8080116 Fax: +49 241 803380116 E-Mail: fgremsede.
Corresponding author: Dipl.-Inf. Felix Gremse, Experimental Molecular Imaging, RWTH University Aachen, Pauwelsstr. 30, 52074 Aachen, Germany. Phone: +49 241 8080116 Fax: +49 241 803380116 E-Mail: fgremsede.
 Global reach, higher impact
Global reach, higher impact